Question
Question: Two equal point charges \[Q=\sqrt{2}\mu C\]are placed at each of the two opposite corners of a squar...
Two equal point charges Q=2μCare placed at each of the two opposite corners of a square and equal point charges q at each of the two corners. What must be the value of q so that the resultant force on Q is zero?
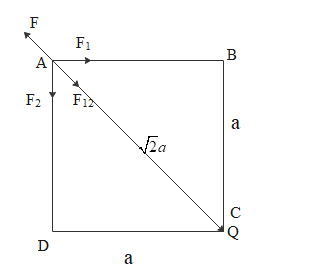
Solution
First of all read the question carefully and understand the values or quantities given in the question. Also observe the diagram carefully. After that apply Coulomb’s law. Since the two forces are acting at right angles we must calculate the resultant force. Then equate it with the force due to Q. Thus by rearranging and substituting the values we get the value of q.
Complete step-by-step solution:
Let the side of the square be ‘a’. Then by Pythagoras theorem the diagonal of the square is 2a.
Thus the force due to the charge Q at A and C is,
F=4πε012a2Q2
And the direction of this force is outward.
Hence in order to become the net force to zero, the force F1 on Q due to q must be equal to the force F2 on Q due to q.
Thus,
F1=F2=4πε01a2Qq
As F1and F2are at right angles.
F12=4πε01a22Qq
For the equilibrium condition of Q,
F=F12
4πε012a2Q2=4πε01a22Qq
⇒2Q=2q
We have to find q. Hence rearranging and substituting the values we get,
q=22Q
∴q=222μC=0.5μC
Note: Remember that the resultant force is the difference in the magnitude of larger force to the smaller force. If the two forces have the same magnitude and if they are acting just in the opposite direction to one another then the resultant force is zero.
