Question

Two equal parabolas have the same focus and their axes are at right angles. A normal to one is perpendicular to normal to the other. Prove that the locus of the point of intersection of these normals is another parabola

Answer 1

Hint: Equation of normal to parabola ${{y}^{2}}=4ax$ is given as $y=mx-2am-a{{m}^{3}}$, where $m$ is the slope of the normal.

We will consider the equation of one of the parabolas as ${{y}^{2}}=4ax$.

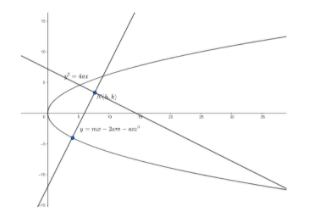
So , its focus is $S\left( a,0 \right)$.
We know, the equation of normal to the parabola in slope form is given as
$y=mx-2am-a{{m}^{3}}....\left( i \right)$ , where $m$ is the slope of the normal.
Now , we have to find the locus of intersection of the normal.
We will consider this point to be $N\left( h,k \right)$.
Now, since $N\left( h,k \right)$ is the point of intersection of the normals , so , it should lie on equation $\left( i \right)$, i.e. the point $N\left( h,k \right)$ should satisfy equation $\left( i \right)$.
So , we will substitute $x=h$ and $y=k$ in equation $\left( i \right)$.
On substituting $x=h$ and $y=k$ in equation $\left( i \right)$ , we get
$k=mh-2am-a{{m}^{3}}$
Or , $a{{m}^{3}}+m\left( 2a-h \right)+k=0....\left( ii \right)$
Clearly, we can see that equation $\left( ii \right)$ is a cubic equation in $m$ , which is of the form $a{{m}^{3}}+b{{m}^{2}}+cm+d=0$. So , it should represent three lines passing through $\left( h,k \right)$.
Now, in the question , it is given that two perpendicular normals pass through $N\left( h,k \right)$. So , out of these three lines , two lines must be perpendicular.
Now , let ${{m}_{1}},{{m}_{2}}$ and ${{m}_{3}}$ be three roots of equation $\left( ii \right)$. The roots of the equation $\left( ii \right)$ are corresponding to the slopes of the three lines.
Now, we are given two of these lines are perpendicular.
We know , when two lines are perpendicular , the product of their slopes is equal to $-1$ .
So, ${{m}_{1}}{{m}_{2}}=-1....\left( iii \right)$
We know , for a cubic equation of the form $a{{m}^{3}}+b{{m}^{2}}+cm+d=0$, the product of the roots is given as $\dfrac{-d}{a}$.
So , from equation $\left( ii \right)$ , we have
${{m}_{1}}{{m}_{2}}{{m}_{3}}=\dfrac{-k}{a}$
Since , ${{m}_{1}}{{m}_{2}}=-1\text{ }\left( \text{from equation }iii \right)$
So, ${{m}_{3}}=\dfrac{k}{a}$
Now , ${{m}_{3}}$ is a root of equation $\left( ii \right)$. So , it should satisfy the equation.
So , $a{{\left( \dfrac{k}{a} \right)}^{3}}+\dfrac{k}{a}\left( 2a-h \right)+k=0$
Or $\dfrac{{{k}^{3}}}{{{a}^{2}}}+2k-\dfrac{kh}{a}+k=0$
Or ${{k}^{2}}+3{{a}^{2}}-ah=0$
Or ${{k}^{2}}=a\left( h-3a \right)$
Now , the locus of $N\left( h,k \right)$ is given by replacing $\left( h,k \right)$ by $\left( x,y \right)$
So, the locus of $N\left( h,k \right)$ is given as ${{y}^{2}}=a\left( x-3a \right)$ which is the equation of a parabola.

Note: The product of slopes of perpendicular lines is equal to $-1$ and not $1$. Students generally get confused and make this mistake.