Question

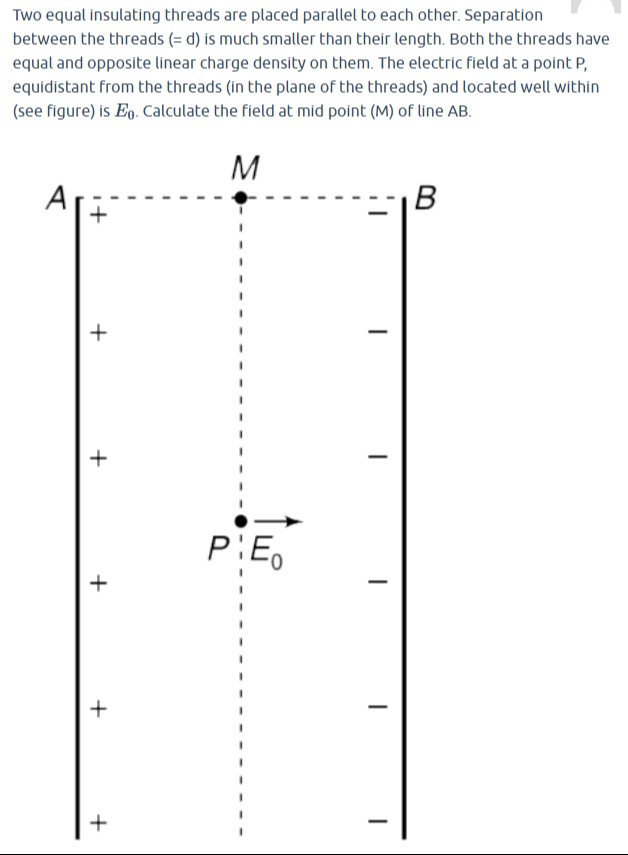
Two equal insulating threads are placed parallel to each other. Separation between the threads (= d) is much smaller than their length. Both the threads have equal and opposite linear charge density on them. The electric field at a point P, equidistant from the threads (in the plane of the threads) and located well within (see figure) is $E_0$. Calculate the field at mid point (M) of line AB.

Answer 1

E_0/sqrt(2)

Answer 2

The problem describes two parallel insulating threads with equal and opposite linear charge densities. Let the linear charge density on the left thread be $+\lambda$ and on the right thread be $-\lambda$. The separation between the threads is $d$. The length of the threads ($L$) is much greater than their separation ($d$), i.e., $L \gg d$. This condition allows us to treat the threads as infinite lines of charge for points far from their ends.

1. Electric field at point P ($E_0$): Point P is equidistant from the threads and located "well within" the threads. This means P is far from the ends, so we can use the infinite line approximation. The electric field due to an infinite line of charge with linear charge density $\lambda$ at a perpendicular distance $r$ is given by: $E = \frac{\lambda}{2 \pi \epsilon_0 r}$

For the left thread (positive $\lambda$), the distance to P is $d/2$. The electric field $E_L$ at P will be directed away from the positive thread, i.e., towards the right. $E_L = \frac{\lambda}{2 \pi \epsilon_0 (d/2)} = \frac{\lambda}{\pi \epsilon_0 d}$ (towards right)

For the right thread (negative $-\lambda$), the distance to P is $d/2$. The electric field $E_R$ at P will be directed towards the negative thread, i.e., towards the right. $E_R = \frac{|-\lambda|}{2 \pi \epsilon_0 (d/2)} = \frac{\lambda}{\pi \epsilon_0 d}$ (towards right)

The total electric field at P, $E_0$, is the vector sum of $E_L$ and $E_R$. Since both are in the same direction: $E_0 = E_L + E_R = \frac{\lambda}{\pi \epsilon_0 d} + \frac{\lambda}{\pi \epsilon_0 d} = \frac{2\lambda}{\pi \epsilon_0 d}$

2. Electric field at point M ($E_M$): Point M is at the mid-point of line AB, where A and B are the top ends of the threads. This means M is located at the end of the thread configuration. Since $L \gg d$, we can approximate the field at M as that due to a semi-infinite line of charge.

The electric field due to a finite line segment of length $L_0$ with uniform linear charge density $\lambda$ at a point P which is at a perpendicular distance $a$ from one end and aligned with that end is given by: $E_{\perp} = \frac{\lambda}{4\pi\epsilon_0 a} \frac{L_0}{\sqrt{L_0^2+a^2}}$ (perpendicular component) $E_{\parallel} = \frac{\lambda}{4\pi\epsilon_0 a} (1 - \frac{a}{\sqrt{L_0^2+a^2}})$ (parallel component)

Since $L_0 \gg a$ (here $L_0$ is the length of the thread and $a = d/2$), we can approximate $\sqrt{L_0^2+a^2} \approx L_0$. So, the formulas simplify to: $E_{\perp} \approx \frac{\lambda}{4\pi\epsilon_0 a} \frac{L_0}{L_0} = \frac{\lambda}{4\pi\epsilon_0 a}$ $E_{\parallel} \approx \frac{\lambda}{4\pi\epsilon_0 a} (1 - \frac{a}{L_0}) \approx \frac{\lambda}{4\pi\epsilon_0 a}$ (since $a/L_0 \ll 1$)

Let's place the left thread along the y-axis from $(0,0)$ to $(0,L_0)$ and the right thread along $x=d$ from $(d,0)$ to $(d,L_0)$. Point M is at $(d/2, L_0)$. For both threads, the perpendicular distance from M to the thread is $a = d/2$.

Field due to the left thread (positive $\lambda$) at M: The perpendicular component $E_{L,x}$ is directed away from the positive thread, i.e., towards the right. $E_{L,x} = \frac{\lambda}{4\pi\epsilon_0 (d/2)} = \frac{\lambda}{2\pi\epsilon_0 d}$ (towards right) The parallel component $E_{L,y}$ is directed away from the positive charge, along the thread. Since M is at the top end, the field component will be downwards. $E_{L,y} = \frac{\lambda}{4\pi\epsilon_0 (d/2)} = \frac{\lambda}{2\pi\epsilon_0 d}$ (downwards)

Field due to the right thread (negative $-\lambda$) at M: The perpendicular component $E_{R,x}$ is directed towards the negative thread, i.e., towards the right. $E_{R,x} = \frac{|-\lambda|}{4\pi\epsilon_0 (d/2)} = \frac{\lambda}{2\pi\epsilon_0 d}$ (towards right) The parallel component $E_{R,y}$ is directed towards the negative charge, along the thread. Since M is at the top end, the field component will be downwards. $E_{R,y} = \frac{|-\lambda|}{4\pi\epsilon_0 (d/2)} = \frac{\lambda}{2\pi\epsilon_0 d}$ (downwards)

Total electric field at M: The total x-component of the electric field at M is: $E_{M,x} = E_{L,x} + E_{R,x} = \frac{\lambda}{2\pi\epsilon_0 d} + \frac{\lambda}{2\pi\epsilon_0 d} = \frac{\lambda}{\pi\epsilon_0 d}$ (towards right)

The total y-component of the electric field at M is: $E_{M,y} = E_{L,y} + E_{R,y} = \frac{\lambda}{2\pi\epsilon_0 d} + \frac{\lambda}{2\pi\epsilon_0 d} = \frac{\lambda}{\pi\epsilon_0 d}$ (downwards)

The magnitude of the total electric field at M is: $E_M = \sqrt{E_{M,x}^2 + E_{M,y}^2} = \sqrt{\left(\frac{\lambda}{\pi\epsilon_0 d}\right)^2 + \left(\frac{\lambda}{\pi\epsilon_0 d}\right)^2}$ $E_M = \sqrt{2 \left(\frac{\lambda}{\pi\epsilon_0 d}\right)^2} = \frac{\lambda}{\pi\epsilon_0 d} \sqrt{2}$

Relating $E_M$ to $E_0$: From the expression for $E_0$: $E_0 = \frac{2\lambda}{\pi \epsilon_0 d} \implies \frac{\lambda}{\pi \epsilon_0 d} = \frac{E_0}{2}$

Substitute this into the expression for $E_M$: $E_M = \left(\frac{E_0}{2}\right) \sqrt{2} = \frac{E_0}{\sqrt{2}}$

The direction of $E_M$ is $45^\circ$ below the horizontal, pointing towards the right and downwards.

The final answer is $\boxed{\frac{E_0}{\sqrt{2}}}$