Question

Two equal charges are separated by a distance d. A third charge placed on a perpendicular bisector at x distance will experience maximum Coulomb force when
A. $x=\dfrac{d}{\sqrt{2}}$
B. $x=\dfrac{d}{2}$
C. $x=\dfrac{d}{2\sqrt{2}}$
D. $x=\dfrac{d}{2\sqrt{3}}$

Answer 1

Use the formula for the Coulomb force between two charges and find the net force on the third charge with the help of trigonometry. Then for the value of x for which the force experienced by the charge is maximum, write the force in terms of x and equate its first derivative to zero.

Formula used:
$F=\dfrac{K{{q}^{2}}}{{{r}^{2}}}$

Complete step by step answer:
It is given that there are two equal charges separated by a distance d. A third charge is placed on the perpendicular bisector of the line segment joining the two charges, at x distance from the midpoint (as shown). Let the third charge be equal to the other two charges.

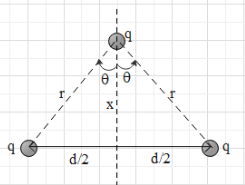
Now, each of the two charges will exert Coulomb force on the third. The magnitude of the Coulomb force that a charge ${{q}_{1}}$ exerts on charge ${{q}_{2}}$, which is at a distance r from charge ${{q}_{1}}$ is given as $F=\dfrac{K{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$, where K is a proportionality constant.

Therefore, the magnitude of force exerted by each charge on the third charge is $F=\dfrac{K{{q}^{2}}}{{{r}^{2}}}$ …. (i), where ${{r}^{2}}={{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}$ as shown in the figure.
(The magnitude of two forces are equal due to symmetry in the system).
Since the two charges in both the pairs are equal, they will repel each other and the force will be along the line joining the charges.

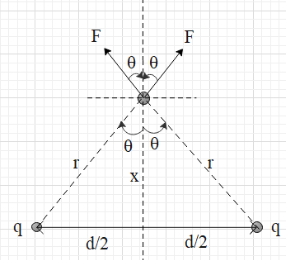
Now, resolve the two forces into the horizontal and vertical components. From the figure we get that horizontal components of each force are ${{F}_{H}}=F\sin \theta$. However, these two forces are opposite in direction. Therefore, the net horizontal force is $F\sin \theta -F\sin \theta =0$.The vertical components of each force (F) are ${{F}_{V}}=F\cos \theta$ and the two are in the same direction. Therefore, the net vertical force is $F\cos \theta +F\cos \theta =2F\cos \theta$.

This means that the net force experienced by the third charge is ${{F}_{net}}=2F\cos \theta$ in the upward direction.
Substitute the value of F from (i).
$\Rightarrow {{F}_{net}}=\dfrac{2K{{q}^{2}}}{{{r}^{2}}}\cos \theta$.
But ${{r}^{2}}={{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}$.
$\Rightarrow {{F}_{net}}=\left( \dfrac{2K{{q}^{2}}}{{{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}} \right)\cos \theta$ …. (iii).
From the figure, we get that $\cos \theta =\dfrac{x}{r}=\dfrac{x}{\sqrt{{{r}^{2}}}}=\dfrac{x}{\sqrt{{{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}}}$.
Substitute this value in (iii).
$\Rightarrow {{F}_{net}}=\left( \dfrac{2K{{q}^{2}}}{{{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}} \right)\dfrac{x}{\sqrt{{{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}}}$
$\Rightarrow {{F}_{net}}=\dfrac{2K{{q}^{2}}x}{{{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{3}{2}}}}$.
Therefore, we found an expression for the force experienced by the third charge.

We can see that the force depends on x. Now to find the value of x where the force is maximum or minimum differentiate it with respect to x and equate to zero.
$\Rightarrow \dfrac{d}{dx}\left( {{F}_{net}} \right)=\dfrac{d}{dx}\left[ \dfrac{2K{{q}^{2}}x}{{{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{3}{2}}}} \right]=0$
On simplifying we get,
$\Rightarrow \dfrac{d}{dx}\left[ \dfrac{2K{{q}^{2}}x}{{{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{3}{2}}}} \right]=\dfrac{2K{{q}^{2}}{{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{3}{2}}}-2K{{q}^{2}}x\left( \dfrac{3}{2}{{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{1}{2}}}.\left( 2x \right) \right)}{{{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{3}}}=0$
$\Rightarrow {{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{3}{2}}}-3{{x}^{2}}{{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{1}{2}}}=0$
$\Rightarrow {{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{1}{2}}}\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}-3{{x}^{2}} \right)=0$

But ${{\left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}} \right)}^{\dfrac{1}{2}}}$ is a positive value. Therefore,
$\Rightarrow \left( {{x}^{2}}+{{\left( \dfrac{d}{2} \right)}^{2}}-3{{x}^{2}} \right)=0$
$\Rightarrow 2{{x}^{2}}-{{\left( \dfrac{d}{2} \right)}^{2}}=0$
$\Rightarrow 2{{x}^{2}}={{\left( \dfrac{d}{2} \right)}^{2}}$
$\Rightarrow {{x}^{2}}=\dfrac{1}{2}{{\left( \dfrac{d}{2} \right)}^{2}}$
$\therefore x=\pm \dfrac{1}{\sqrt{2}}\left( \dfrac{d}{2} \right)$
But x is a distance and distance is always positive. Hence, $x=-\dfrac{1}{\sqrt{2}}\left( \dfrac{d}{2} \right)$ is discarded. This means that $x=\dfrac{d}{2\sqrt{2}}$. We can understand that the net force on the charge at $x=0$ is zero. This means that as the value of x increases the force also increases because at $x=\dfrac{d}{2\sqrt{2}}$, the force is greater than zero. Therefore, we can say that at $x=\dfrac{d}{2\sqrt{2}}$ the force is maximum.

Hence, the correct option is C.

Note: The derivative of a function with respect to the variable on which it depends is the tangent to the curve at that point.The function can have a maximum or minimum when the tangent to the curve that point is zero. Note that we cannot tell whether the function is maximum or minimum if the derivative is zero because it can be any one of the two. For further confirmation, the second derivative is found. If the second derivative is negative, the function is at its maxima and if the second derivative is positive, the function is at its minima.
In this question, we could tell that the value was maximum because we knew that at $x=0$ the force was zero and it increased as x increased.