Question
Question: Two equal and opposite charges are placed at a certain distance. The force between them is F. If 25%...
Two equal and opposite charges are placed at a certain distance. The force between them is F. If 25% of one charge is transferred to other, then the force between them is:
& \text{A}\text{. F} \\\ & \text{B}\text{. }\dfrac{9F}{16} \\\ & \text{C}\text{. }\dfrac{15F}{16} \\\ & \text{D}\text{. }\dfrac{4F}{15} \\\ \end{aligned}$$Solution
It is given that two equal and opposite charges are placed at a certain distance therefore they will have Coulomb’s force of attraction. Hence by using Coulomb's law we can solve the given question. Here will get two equations one when the charges are equal and second when 25% of one charge is transferred to another charge.
Formula used:
F=4πε01r2q1q2
Complete step by step answer:
If two charges q1 and q2 are separated by a distance r then according to Coulomb’s law the force between them is given by
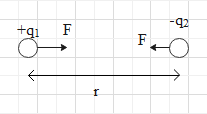
F=4πε01r2q1q2
Here ε0is permittivity in free space.
Now according to question the charges are equal therefore we can write
q1=q2=q
Hence force between them is given as
