Solveeit Logo
Login

Question

Question: Two electrons are moving towards each other each with a velocity of \( {10^6}m/s \) . What will be t...

Two electrons are moving towards each other each with a velocity of 106m/s{10^6}m/s . What will be the closest distance of approach between them?
(A) 1.53×10−8m1.53 \times {10^{ - 8}}m
(B) 2.53×10−10m2.53 \times {10^{ - 10}}m
(C) 2.53×10−6m2.53 \times {10^{ - 6}}m
(D) zerozero

Explanation

Solution

With the decrease in kinetic energy, the potential energy will increase. knowing this we will put the kinetic energy of two electrons equal to their potential energy. then we will solve for the closest distance of approach between them.
The total kinetic energy of electrons, Kinetic  Energy=12mν2Kinetic\;Energy = \dfrac{1}{2}m{\nu ^2}
The potential energy of electrons, Potential  Energy=14πε0q1q2rPotential\;Energy = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{r}
14πε0=9×109Nm2C2\dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}\dfrac{{N{m^2}}}{{{C^2}}}
e=1.6×10−19Ce = 1.6 \times {10^{ - 19}}C
m=9.1×10−31kgm = 9.1 \times {10^{ - 31}}kg .

Complete answer:

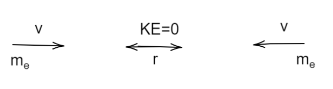
Two electrons of the same mass are moving towards each other with the same velocity ν=106m/s\nu = {10^6}m/s . So at the same time, they will come to zero, when the distance between them is about rr which is the closest distance of approach between them then kinetic energy will be zero.
Therefore, for two electrons, When they approach the closest distance the total kinetic energy of the two electrons will get converted into potential energy of electrons. Hence, the closest distance of approach is when its total kinetic energy is converted into potential energy.
Gain in potential energy == Loss in kinetic energy
14πε0e2r=12mν2+12mν2\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{e^2}}}{r} = \dfrac{1}{2}m{\nu ^2} + \dfrac{1}{2}m{\nu ^2}
Since, (q1=q2=e)\left( {{q_1} = {q_2} = e} \right)
e=1.6×10−19Ce = 1.6 \times {10^{ - 19}}C is the charge of electron
r=r = is the distance between the electrons
m=9.1×10−31kgm = 9.1 \times {10^{ - 31}}kg is the mass of electron
14πε0=9×109Nm2C2\dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}\dfrac{{N{m^2}}}{{{C^2}}}
ν=\nu = is the velocity of electrons
⇒14πε0e2r=mν2\Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{e^2}}}{r} = m{\nu ^2}
For finding the closest distance of approach between them,
⇒r=14πε0e2mν2\Rightarrow r = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{e^2}}}{{m{\nu ^2}}}
Putting all the values from above
⇒r=9×109×(1.6×10−19)29.1×10−31×(106)2\Rightarrow r = \dfrac{{9 \times {{10}^9} \times {{\left( {1.6 \times {{10}^{ - 19}}} \right)}^2}}}{{9.1 \times {{10}^{ - 31}} \times {{\left( {{{10}^6}} \right)}^2}}}
⇒r=2.53×10−10m\Rightarrow r = 2.53 \times {10^{ - 10}}m
Hence option B) 2.53×10−10m2.53 \times {10^{ - 10}}m is the correct option.

Note:
The energy held in an object as a result of its position or arrangement is known as potential energy. Kinetic energy is the energy released by an object as a result of its movement, or motion. Kinetic energy can be turned into potential energy, and potential energy can be converted back into kinetic energy.