Question

Two electric trains run at the same speed of $72\;{\rm{km}}{{\rm{h}}^{ - 1}}$ along the same track and in the same direction with a separation of $2.4\;{\rm{km}}$ between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of $500\;{\rm{m}}$ from the track and is equidistant from the two trains at the instant of the whistling. If both the whistle were at $500\;{\rm{Hz}}$ and the speed of the sound in air is $340\;{\rm{m}}{{\rm{s}}^{ - 1}}$, find the frequencies heard by the person.

Answer 1

First, we will draw the diagram of the given condition for a better understanding of the solution. Then we will use the trigonometry for the determination of the instantaneous speed of the train towards the person. After this, we can find the required frequencies with the help of simple expression.

Complete step by step answer:
It is given to us that the distance between the two trains is $2.4\;{\rm{km}}$, the trains run at the same speed of $72\;{\rm{km}}{{\rm{h}}^{ - 1}}$ and the person is situated at equidistant from the trains and at a perpendicular distance of $500\;{\rm{m}}$ from the track. The frequencies of the whistles were $500\;{\rm{Hz}}$, and the speed of the sound is $340\;{\rm{m}}{{\rm{s}}^{ - 1}}$, so we will use this information for making diagram and calculation.
We will draw the diagram of the given condition, so

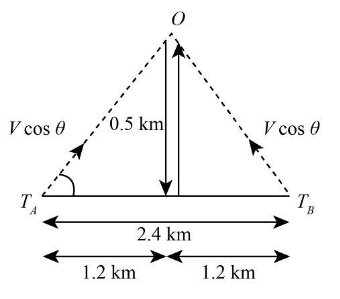
From the above diagram, we can calculate the distance of the person form each train by trigonometry; therefore, we get
$\Rightarrow D = \sqrt {{{\left( {1.2\;{\rm{km}}} \right)}^2} + {{\left( {0.5\;{\rm{km}}} \right)}^2}} \\\ \Rightarrow D = \sqrt {1.44\;{\rm{k}}{{\rm{m}}^2} + 0.25\;{\rm{k}}{{\rm{m}}^2}} \\\ \Rightarrow D = 1.3\;{\rm{km}}$
Now we will calculate the instantaneous speed of the train towards the person, so write the expression for the instantaneous speed of the train.
$\Rightarrow { v_s} = v\cos \theta$
Put $\cos \theta = \dfrac{{1.2\;{\rm{km}}}}{{1.3\;{\rm{km}}}}$ and $v = 72\;{\rm{km}}{{\rm{h}}^{ - 1}}$ in the above equation.

$$\Rightarrow {v_s} = \left( {72\;{\rm{km}}{{\rm{h}}^{ - 1}} \times \dfrac{{1000\;{\rm{m}}}}{{1\;{\rm{km}}}} \times \dfrac{{1\;{\rm{h}}}}{{3600\;{\rm{s}}}}} \right)\dfrac{{\left( {1.2\;{\rm{km}} \times \dfrac{{1000\;{\rm{m}}}}{{1\;{\rm{km}}}}} \right)}}{{\left( {1.3\;{\rm{km}} \times \dfrac{{1000\;{\rm{m}}}}{{1\;{\rm{km}}}}} \right)}}\\\ \Rightarrow {v_s} = 20\;{\rm{m}}{{\rm{s}}^{ - 1}} \times 0.923\\\ \Rightarrow {v_s} = 18.46\;{\rm{m}}{{\rm{s}}^{ - 1}}$$

We obtained the instantaneous speed of the train towards the person and it is given that the speed of the sound is $340\;{\rm{m}}{{\rm{s}}^{ - 1}}$ and frequency of the whistle is $500\;{\rm{Hz}}$, so we will write the expression of the apparent frequency received by the stationary person from the train approaching towards him.
Therefore, we get
$\Rightarrow f = {f_o}\left( {\dfrac{{{v_{sound}}}}{{{v_{sound}} - {v_s}}}} \right)$
Here,${v_{sound}}$is the speed of sound and ${f_o}$ is the frequency of the whistle.
Substitute the values in the above equation.

$$\Rightarrow f = 500\;{\rm{Hz}}\left( {\dfrac{{340\;{\rm{m}}{{\rm{s}}^{ - 1}}}}{{340\;{\rm{m}}{{\rm{s}}^{ - 1}} - 18.46\;{\rm{m}}{{\rm{s}}^{ - 1}}}}} \right)\\\ \Rightarrow f = 500\;{\rm{Hz}} \times {\rm{1}}{\rm{.05}}\\\ \Rightarrow f = 525\;{\rm{Hz}}$$

Now, we will write the expression of the apparent frequency received by the stationary person from the train going away from him.
$f = {f_o}\left( {\dfrac{{{v_{sound}}}}{{{v_{sound}} + {v_s}}}} \right)$
Substitute the values in the above equation.

$$\Rightarrow f = 500\;{\rm{Hz}}\left( {\dfrac{{340\;{\rm{m}}{{\rm{s}}^{ - 1}}}}{{340\;{\rm{m}}{{\rm{s}}^{ - 1}} + 18.46\;{\rm{m}}{{\rm{s}}^{ - 1}}}}} \right)\\\ \Rightarrow f = 500\;{\rm{Hz}} \times 0.95\\\ \Rightarrow f = 475\;{\rm{Hz}}$$

Therefore, the frequencies heard by the person are $525\;{\rm{Hz}}$ and $475\;{\rm{Hz}}$.

Note: In these types of questions, always remember that the expressions of the apparent frequency for the train coming towards the stationary person and train going away from the stationary person, because expressions of the frequency are almost the same with the slight difference of sign.