Question

Two electric dipoles of moment $P$ and $64P$ are placed in opposite directions on a line at a distance of $25cm$. The electric field will be zero at point between the dipoles whose distance from the dipole of moment $P$ is
A.$5cm$
B.$\dfrac{25}{9}cm$
C.$10cm$
D.$\dfrac{4}{13}cm$

Answer 1

We are given two dipoles of different magnitudes which are inclined along the axial position with respect to each other. The electric field due to these two dipoles must be equal to zero at some point between the two dipoles on the line joining them. Thus, we shall apply the formula of electric field on the dipoles given and then find the distance x from dipole $P$at which the electric field is zero.

Complete answer:
The electric field $\left( {\vec{E}} \right)$ due to an electric dipole at axial position is given as:
$\vec{E}=\dfrac{2kp}{{{r}^{3}}}$
Where,
$k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}$ and ${{\varepsilon }_{0}}=8.85\times {{10}^{-12}}F{{m}^{-1}}$ is the permittivity of free space
$p=$ magnitude of dipole moment
$r=$ distance between dipole and point of observation
Let the electric field be zero at a distance $x$ from dipole $P$.

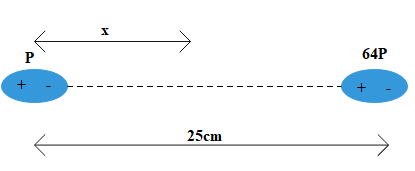
For dipole 1, we have $p=P$ and $r=x$,
Substituting these values, we get
$\vec{E}=\dfrac{2kP}{{{x}^{3}}}$ ……………….. equation (1)
For dipole 2, we have $p=64P$ and $r=25-x$,
Substituting these values, we get
$\vec{E}=\dfrac{2k\left( 64P \right)}{{{\left( 25-x \right)}^{3}}}$ ……………….. equation (2)
Since the electric field at distance $x$ is zero, thus we shall take the net electric fields due to both dipoles at this point and equate it to zero.
From equation (1) and (2), we have
$\dfrac{2kP}{{{x}^{3}}}-\dfrac{2k\left( 64P \right)}{{{\left( 25-x \right)}^{3}}}=0$
Taking $2,k,P$ common in both terms and cancelling them with zero, we get
$\dfrac{1}{{{x}^{3}}}-\dfrac{64}{{{\left( 25-x \right)}^{3}}}=0$
We shall now transpose one term to the right-hand side and simplify further.
$\Rightarrow \dfrac{1}{{{x}^{3}}}=\dfrac{64}{{{\left( 25-x \right)}^{3}}}$
$\Rightarrow {{\left( 25-x \right)}^{3}}=64{{x}^{3}}$
We know that $64=4\times 4\times 4$, it can also be written as $64={{4}^{3}}$. Thus, substituting this value of 64, we get
$\begin{aligned} & \Rightarrow {{\left( 25-x \right)}^{3}}={{4}^{3}}.{{x}^{3}} \\\ & \Rightarrow {{\left( 25-x \right)}^{3}}={{\left( 4x \right)}^{3}} \\\ \end{aligned}$
Now, king cube roots on both sides, we get
$\begin{aligned} & \Rightarrow \sqrt[3]{{{\left( 25-x \right)}^{3}}}=\sqrt[3]{{{\left( 4x \right)}^{3}}} \\\ & \Rightarrow 25-x=4x \\\ \end{aligned}$
Here, we have a linear equation in variable-x. Thus, transposing -x to the right-hand side, we get
$\Rightarrow 25=4x+x$
$\Rightarrow 25=5x$
Dividing both sides by 5, we get
$\begin{aligned} & \Rightarrow \dfrac{5x}{5}=\dfrac{25}{5} \\\ & \Rightarrow x=5 \\\ \end{aligned}$
Therefore, the electric field will be zero at a point between the dipoles whose distance from the dipole of moment $P$ is $5cm$.

Therefore, the correct option is (B) $5cm$.

Note:
One possible mistake we could have done was expanding the expression raised to the power of 3 using the mathematical properties. If we would have expanded the expression, ${{\left( 25-x \right)}^{3}}$, then the equation would have become very complex consisting of 2-degree and 3-degree variables also which would have become very difficult to solve.