Question

Two electric bulbs A and B rated $200V \sim 100W$ and $200V \sim 60W$ are connected in series to a $200V$ line. Then the potential drop across
(A) Each bulb is $200V$
(B) $100W$ Bulb is greater than that across $60W$ bulb
(C) $100W$ Bulb is smaller than that across $60W$ bulb
(D) Each bulb is $100V$

Answer 1

First we construct a circuit diagram of the given two bulbs connected in series. By using the equation power $(P) = \dfrac{{{V^2}}}{R}$ we will find the resistance of the respective bulb and by using that resistance we will obtain the Current $(I)$ flowing through the circuit. Now by using the ohm's law $V = IR$we will find the potential difference $(V)$ across each bulb.
Formula used:
$\Rightarrow {P_A} = \dfrac{{{V^2}}}{{{R_A}}}$
$\Rightarrow I = \dfrac{V}{R}$

Complete step by step solution:

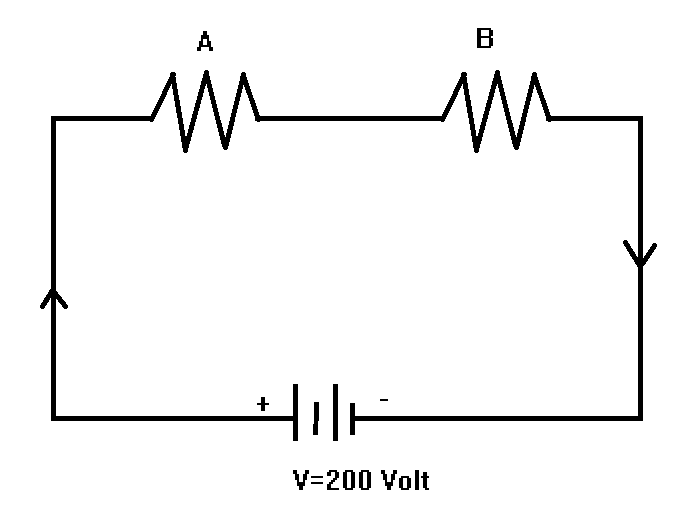
Here we will first obtain the resistance of the respective bulb by using the formula of power $(P) = \dfrac{{{V^2}}}{R}$
For bulb A the resistance,
$\Rightarrow {P_A} = \dfrac{{{V^2}}}{{{R_A}}}$
$\Rightarrow {R_A} = \dfrac{{{V^2}}}{{{P_A}}}$ --------- Equation $(1)$
For Bulb a Power is $100W$ , Voltage is $200V$ , hence substituting the values of $P$ and $V$ in the equation $(1)$
$\Rightarrow {R_A} = \dfrac{{{{(200)}^2}}}{{100}}$
$\therefore {R_A} = 400\Omega$
Similarly for Bulb B Power is 60 W, Voltage is 200 V, hence substituting the values of P and V in equation (1)
$\Rightarrow {R_B} = \dfrac{{{{(200)}^2}}}{{60}}$
$\therefore {R_B} = 666.67\Omega$
Now as both the bulb are connected in series the total resistance ${R_{Total}}$of the circuit can be given as
$\Rightarrow {R_{Total}} = {R_A} + {R_B}$
Putting the values in the above equation we get,
$\Rightarrow {R_{Total}} = 400\Omega + 666.67\Omega$
$\therefore {R_{Total}} = 1066.67\Omega$
Now according to Ohm's law, the Voltage $(V)$ across any conductor is directly proportional to the current $(I)$ flowing through it at a constant temperature. Hence,
$\Rightarrow V \propto I$
$\Rightarrow V = RI$
Where R is constant of proportionality also known as resistance, Hence
$\Rightarrow I = \dfrac{V}{R}$
$\Rightarrow I = \dfrac{V}{{{R_{Total}}}}$ -----------equation $(2)$
Given $V = 200V$ across the circuit and ${R_{Total}} = 1066.67\Omega$ putting in the equation $(2)$
$\Rightarrow I = \dfrac{{200V}}{{1066.67\Omega }}$
$\Rightarrow I = 0.18799A \simeq 0.1875A$
Now the potential difference across each bulb A and B by using the formula $V = RI$
For bulb A the ${R_A} = 400\Omega$
$\Rightarrow {V_A} = {R_A}I$
$\Rightarrow {V_A} = 400 \times 0.1875 = 75\Omega$
For bulb B the ${R_B} = 667.67\Omega$
$\Rightarrow {V_B} = {R_B}I$
$\Rightarrow {V_B} = 666.67 \times 0.1875 = 125\Omega$
Here on comparing the potential difference of both bulb A and B
$\therefore {V_A} < {V_B}$

Hence, option (C) is the correct answer.

Note: Here we have to note that both the bulbs are connected in the circuits behaving as a source of resistance that’s why we used ohm's law. Similarly, if the bulbs are connected in parallel connection then we can find the total resistance ${R_{total}}$can be found by the formula$\dfrac{1}{{{R_{Total}}}} = \dfrac{1}{{{R_A}}} + \dfrac{1}{{{R_B}}}$.