Question

Two discs of the same moment of inertia rotating about their regular axis passing through the centre and perpendicular to the plane of a disc with angular velocities $\omega_1$ and $\omega_2$. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is:
A. $\dfrac{I}{4}(\omega_1 - \omega_2)^2$
B. $I(\omega_1 - \omega_2)^2$
C. $\dfrac{I}{8}(\omega_1 - \omega_2)^2$
D. $\dfrac{I}{2}(\omega_1 - \omega_2)^2$

Answer 1

Begin by using the relation between moment of inertia and angular velocity to find the initial angular momenta and kinetic energy of the discs. Add the two individual momenta to get the total initial angular momentum. Now, when they are brought in contact with each other, the two discs behave as one massive unit. In this case, determine the sum of their moments of inertia and obtain an expression for the total final angular momentum and kinetic energy of the system.
Use the conservation of angular momentum principle to equate the two expressions and arrive at the appropriate angular speed of the collective motion of the discs. The loss in energy can be found by plugging in this angular speed expression into the difference between the initial and final kinetic energies, which is what we require to the end.
Formula Used:
Angular momentum: $L=I\omega$
Conservation of angular momentum: $L_i=L_f$
Kinetic energy $K = \dfrac{1}{2}I\omega^2$

Complete step by step answer:
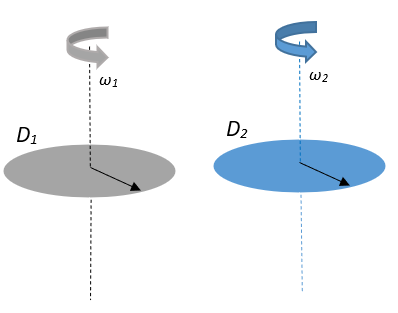
We have two discs, say $D_1$ and $D_2$, with their axes of rotation passing through their centre, perpendicular to their plane, as shown in the figure. They are rotated about their axes of rotation with angular velocities of $\omega_1$ and $\omega_2$ respectively such that their moments of inertia about their axes of rotation are the same, i.e.,
$I_1 = I_2 = I$

Now, the angular momentum of a disc is given as:
$L=I\omega$
The total initial angular momentum of two discs will be the sum of their individual angular momenta, i.e.,
$L_i = I_1\omega_1 + I_2\omega_2 = I\omega_1 + I\omega_2$
The kinetic energy of a disc is given as:
$K = \dfrac{1}{2}I\omega^2$
The total initial kinetic energy of two discs will be the sum of their individual kinetic energies, i.e.,
$K_i = \dfrac{1}{2} I_1\omega_1^2 + \dfrac{1}{2}I_1\omega_2^2 = \dfrac{1}{2} I\omega_1^2 + \dfrac{1}{2}I\omega_2^2 = \dfrac{1}{2} I (\omega_1^2 + \omega_2^2)$
Now, the two discs are brought in contact face to face, with their axes of rotation coincident. This means that the moment of inertia of the system becomes the sum of their individual moments of inertia. This results in the two discs moving with a new mutual angular velocity, say $\omega$.

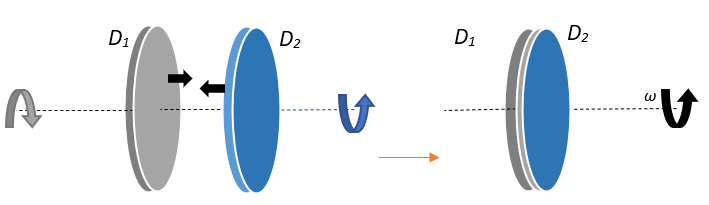
The total final angular momentum of the system of two discs in contact with each other will be,
$L_f = (I_1+I_2)\omega = (I+I)\omega = 2I\omega$
The total final kinetic energy of the system of two discs in contact with each other will be,
$K_f = \dfrac{1}{2}(I_1+I_2)\omega^2 = \dfrac{1}{2}(I+I)\omega^2 = \dfrac{1}{2}2I\omega^2 = I\omega^2$
According to the law of conservation of angular momentum, for any isolated system, the total initial and final angular momentum will remain constant, i.e.,
$L_i=L_f$
$\Rightarrow I\omega_1 + I\omega_2 = 2I\omega$
$\Rightarrow \omega = \dfrac{1}{2}(\omega_1 + \omega_2)$ ….. (1)
Now, the loss in energy can be given as:
$\Delta K = K_i – K_f$
$\Rightarrow \Delta K = \dfrac{1}{2} I (\omega_1^2 + \omega_2^2) - I\omega^2$
Plugging in (1) into the above equation, we get:
$\Delta K = \dfrac{1}{2} I (\omega_1^2 + \omega_2^2) - I\left(\dfrac{1}{2}(\omega_1 + \omega_2)\right)^2$
$\Rightarrow \Delta K = \dfrac{I}{2} (\omega_1^2 + \omega_2^2) – \dfrac{I}{4}\left(\omega_1^2 + \omega_2^2 + 2\omega_1 \omega_2\right)$
$\Rightarrow \Delta K = \dfrac{I}{2}\omega_1^2 + \dfrac{I}{2}\omega_2^2 - \dfrac{I}{4}\omega_1^2 - \dfrac{I}{4}\omega_2^2 - \dfrac{I}{4}2\omega_1\omega_2$
$\Rightarrow \Delta K = \dfrac{I}{4}\left(\omega_1^2 + \omega_2^2 – 2\omega_1\omega_2\right)$
$\Rightarrow \Delta K = \dfrac{I}{4}\left(\omega_1 -\omega_2\right)^2$

So, the correct answer is “Option A”.

Note: It is important to understand the collective behaviour of components and the factors that get influenced under their non-individualistic behaviour. We add up the moments of inertia in the second case to signify the repositioning of the centre of mass of the entire system, since it now behaves as a collective unit with the two discs working together. This also influences their rotatory motion which is why we get a kind of a superposed final angular speed.
Also, always pay attention to the mentioned axis of rotation, since the expression for the moment of inertia for the same object will differ if it has a different axis of rotation. Suppose the axis of rotation of the disc was at the rim of the disc, then its moment of inertia would be $I = \dfrac{3}{2}mr^2$, or if its axis of rotation was along the diameter of the disc, it would be $I=\dfrac{1}{4}mr^2$ and so on.