Question

Two dipoles each of moment $5 \times {10^{ - 12}}Cm$ form a cross with their axis (- to +) along the coordinate axes. The potential at a point $20cm$ away in a direction making an angle of ${30^ \circ }$ with axis is
A. 1.12 V
B. 2.12 V
C. 2.4 V
D. 1.536 V

Answer 1

Electric dipole is defined as the separation of positive and negative charges. Electric potential energy is defined as the amount of work needed to move a unit positive charge from a point to a specific point in an electric field. We will find the electric potential due to both of the dipoles then find the required solution which is the potential at a point $20cm$ away in a direction making an angle of ${30^ \circ }$ with the axis.
Formula Used:
$V = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{{p\cos \theta }}{{{r^2}}}$

Complete answer:
We will create a rough diagram of the two dipoles which are crossing each other for a better understanding of the given question.

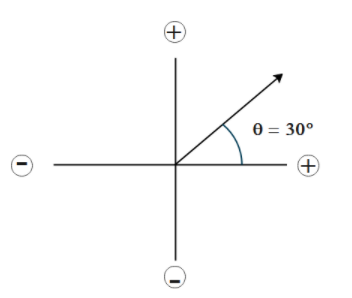
An electric potential due to dipole at a point which is far away from the dipole is given as,
$V = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{{p\cos \theta }}{{{r^2}}}$
where V represents the electric potential,
and p represents the dipole moment.
Now, electric potential due to first dipole is given by,
${V_1} = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{{p\cos \theta }}{{{r^2}}}$ ; where it is given that $\theta = {30^ \circ }$
$\Rightarrow {V_1} = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{{p\cos \left( {{{30}^ \circ }} \right)}}{{{r^2}}}$
$\Rightarrow {V_1} = \dfrac{{9 \times {{10}^9} \times 5 \times {{10}^{ - 12}} \times \cos {{30}^ \circ }}}{{{{\left( {0.2} \right)}^2}}}$
${V_1} = 0.97425V$
Similarly, electric potential due to second dipole is given by,
${V_2} = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{{p\cos \theta }}{{{r^2}}}$; where value of ‘$\theta$’ will be $\theta = 270 + {30^ \circ }$
$\Rightarrow {V_2} = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{{p\cos \left( {{{270}^ \circ } + {{30}^ \circ }} \right)}}{{{r^2}}}$
Now, we know that $\cos \left( {{{270}^ \circ } + \theta } \right) = \sin \theta$
So,
$\Rightarrow {V_2} = \dfrac{{9 \times {{10}^9} \times 5 \times {{10}^{ - 12}} \times \sin {{30}^ \circ }}}{{{{\left( {0.2} \right)}^2}}}$
${V_2} = 0.5625V$
Thus, total potential of the two dipoles is given by,
$\Rightarrow V = {V_1} + {V_2}$
$= \left( {0.97425 + 0.5625} \right)V = 1.536V$
Therefore, the potential at a point $20cm$ away in a direction making an angle of ${30^ \circ }$ with axis is 1.536V.

Hence, option (D) is the correct answer.

Note:
Electric dipole is known as the couple of opposite charges q and -q which is separated by distance ‘r’. An electric dipole moment is defined as the product of the magnitude of the charge and the distance between the centres of the positive and negative charges.
Mathematically it is given as, $\mu = Q \times r$
Where ‘Q’ is expressed as the charge and ‘r’ is the distance.