Question

Two diametrically opposite points of a metal ring are connected to two terminals of the left gap of metre bridge. The resistance of $11\Omega$ is connected in the right gap. If a null point is obtained at a distance of 45cm from the left end, find the resistance of the metal ring.

Answer 1

In this question we have to apply the concept of resistance, combinations of resistors and the metre bridge. We have to convert the given question into a combination of resistors and then use the combinations to calculate the resistance in the other gap of metre bridge using the formula of metre bridge.

Complete step by step answer:
We can assume the resistance of the complete ring to be 2R. If we make a connection in two diametrically opposite ends then we can assume the ring to be two half rings connected to the two terminals. This combination is equivalent to two resistors connected in parallel to the two diametrically opposite terminals with half the resistance of the total ring, i.e. R
The above scenario can be explained by the following diagram.


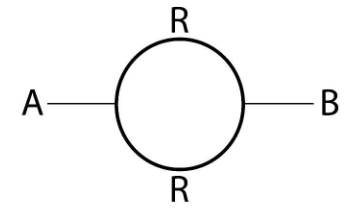
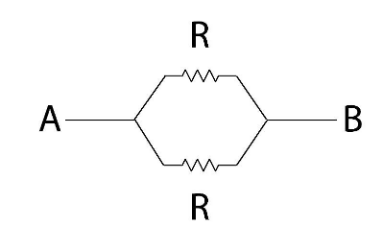
After establishing this diagram, we can easily understand that this is a combination of resistors in parallel combinations with both resistors with value R.
This circuit is connected to the left gap of the metre bridge, but before that we should calculate the equivalent resistance. Of the above ring -setup.
The resistance in this parallel combination is given by:

$$\Rightarrow\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{R} + \dfrac{1}{R}\\\ \Rightarrow\dfrac{1}{{{R_{eq}}}} = \dfrac{2}{R}\\\ \Rightarrow{R_{eq}} = \,\dfrac{R}{2}\Omega$$

Resistance of $\dfrac{R}{2}\Omega$ is connected to the left gap of the metre bridge, for a condition of balanced metre bridge the following condition should be satisfied:
$\dfrac{{{\rm{Resistance in the left gap}}}}{{{\rm{Resistance in the right gap}}}} = \,\dfrac{l}{{100 - l}}$
Given in the question
The resistance in the right gap = $11\Omega$
Length of null point $l$ = 45 cm, and $100 - l = 55$cm
After obtaining all these values we will put it in the formula,
$\Rightarrow\dfrac{{R/2}}{{11}} = \dfrac{{45}}{{55}}\\\ \Rightarrow\dfrac{R}{2} = \dfrac{{45}}{5}\\\ \therefore R = 18\Omega$
The resistance of half the ring is $18\Omega$, therefore the resistance of the total ring is $36\Omega$.

Note: This question can be solved if we assume the ring to be a combination of resistors. If we consider the total resistance of the ring to be R then the calculation will be difficult in comparison if we take the resistance to be 2R.