Question

Two devices of rating $44\,W,220\,V$ and $11\,W$,$220\,V$ are connected in series. The combination is connected across a $440\,V$ main. The fuse of which of the two devices is likely to burn when the switch is ON? Justify your answer.

Answer 1

Let us get some idea about the fuse. A fuse is an electrical safety device that protects an electrical circuit from overcurrent damage. Its most important aspect is a metal wire or strip that melts when too much current flows through it, causing the current to stop or interrupt.

Complete step by step answer:
Before solving the problem let us understand about Electrical power. The rate at which energy is transmitted to or from a portion of an electric circuit is referred to as electric power. Energy can be delivered by a battery or released as heat by a circuit element such as a resistor. The power is proportional to the voltage difference across the element multiplied by the current for each circuit element.
$\text{Electric power}= \text{voltage difference} \times \text{current}$
$\text{Electric power} = {\text{(Current)}^2} \times \text{resistance}$
$\text{Electric power}= \dfrac{{{{\text{(voltage difference)}}^2}}}{{resis\tan ce}}$
$P = {I^2}R = \dfrac{{{V^2}}}{R}$
Given:

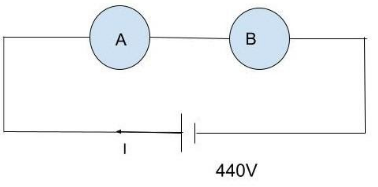
Power of device A (${P_A}$)$=$ $44\,W$
Voltage of device A (${V_A}$)$= 220\,V$
Power of device B (${P_B}$)$= 11\,W$
Voltage of device B (${V_B}$)$= 220\,V$
As we saw above that the power is given as:
$P = \dfrac{{{V^2}}}{R}$
$\Rightarrow {P_A} = \dfrac{{{V_A}^2}}{{{R_A}}}$
$\Rightarrow {R_A} = \dfrac{{{V_A}^2}}{{{P_A}}} \\\ \Rightarrow {R_A}= \dfrac{{{{(220)}^2}}}{{44}} \\\ \Rightarrow {R_A}= 1100\,\Omega$
$\Rightarrow {R_B} = \dfrac{{{{(220)}^2}}}{{11}} = 4400\,\Omega$
According to the problem A & B are in series. So, their equivalent resistance R is:
$R = {R_A} + {R_B} \\\ \Rightarrow R = 5500\,\Omega \\\$

Now, current in the circuit is:
$I = \dfrac{V}{R} \\\ \Rightarrow I= \dfrac{{440}}{{5500}} \\\ \Rightarrow I= 0.08\,A$
Now, let find the voltages:
$\text{Voltage across device A}= I \times {R_A} \\\ \Rightarrow \text{Voltage across device A} = 0.08 \times 1100 \\\ \therefore \text{Voltage across device A} = 88\,V \\\$
$\Rightarrow \text{Voltage across device B}= I \times {R_B} \\\ \Rightarrow \text{Voltage across device B} = 0.08 \times 4400 \\\ \therefore \text{Voltage across device B} = 352\,V \\\$
So we can see from the above calculation that the voltage across B is much greater than voltage across A. So the fuse of device B is more likely to burn first.

Note: In houses, parallel circuits are used so loads can run independently. If a series circuit is used, for example, the lights will become dimmer as more lights are added. If a parallel circuit is used instead of a series circuit, the load receives the maximum power of the circuit.