Question
Question: Two cylindrical conductors A and B, made of the same material, but of length $l$ and $2l$, and diame...
Two cylindrical conductors A and B, made of the same material, but of length l and 2l, and diameter d and 2d, are connected in parallel across a battery. The drift speed of charge carriers inside the conductors is vA and vB respectively, and the rate of heat dissipation in the conductors is HA and HB respectively. Which of these options is/are correct?
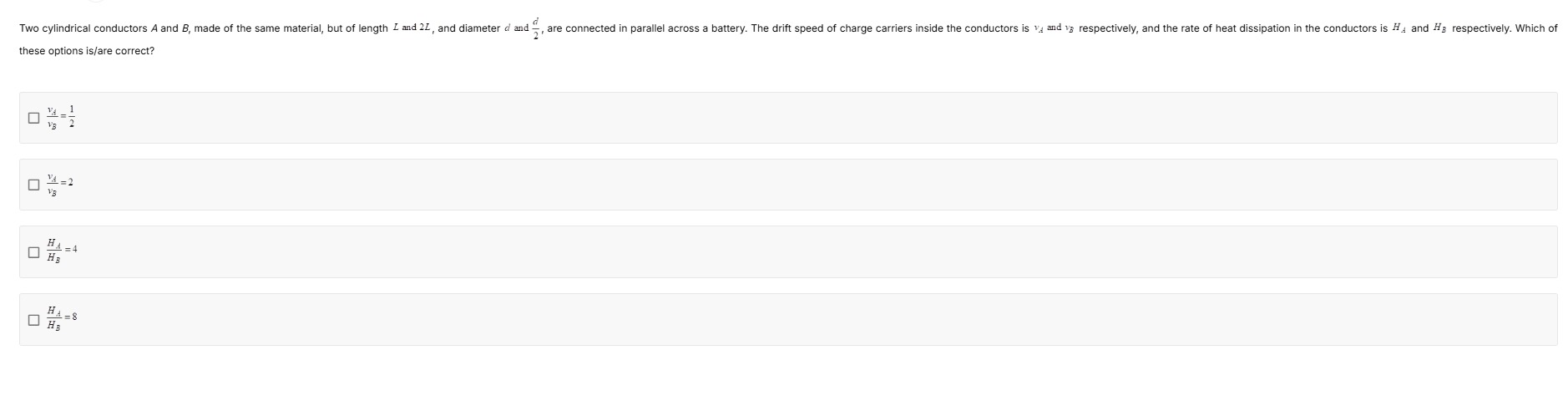
vBvA=21
vBvA=2
HBHA=4
HBHA=8
vBvA=2,HBHA=8
Solution
The problem involves two cylindrical conductors connected in parallel, meaning the potential difference across them is the same. We need to find the ratio of their drift speeds and the ratio of their rates of heat dissipation.
1. Calculate the Resistance of Each Conductor:
The resistance R of a conductor is given by R=ρAL, where ρ is the resistivity, L is the length, and A is the cross-sectional area. The cross-sectional area of a cylinder is A=π(2D)2=4πD2, where D is the diameter.
For conductor A: Length LA=l Diameter DA=d Area AA=4πd2 Resistance RA=ρ4πd2l=πd24ρl
For conductor B: Length LB=2l Diameter DB=2d Area AB=4π(2d)2=4π4d2=16πd2 Resistance RB=ρ16πd22l=πd232ρl
Now, let's find the ratio of their resistances:
RBRA=πd232ρlπd24ρl=324=81So, RB=8RA.
2. Calculate the Ratio of Drift Speeds (vA/vB):
The current I flowing through a conductor is related to the drift speed vd by the formula I=nAvde, where n is the number density of charge carriers and e is the elementary charge. From Ohm's Law, I=RV, where V is the potential difference across the conductor. Equating these two expressions for current:
RV=nAvdeThus, the drift speed vd=RnAeV.
Since the conductors are connected in parallel, the potential difference V across them is the same. They are made of the same material, so the number density of charge carriers n is the same for both. The elementary charge e is a constant. Therefore, the drift speed is inversely proportional to the product of resistance and cross-sectional area (vd∝RA1).
Let's calculate the product RA for each conductor: For conductor A:
RAAA=(πd24ρl)(4πd2)=ρlFor conductor B:
RBAB=(πd232ρl)(16πd2)=2ρlNow, find the ratio of drift speeds:
vBvA=RBAB1RAAA1=RAAARBAB=ρl2ρl=2So, vBvA=2.
3. Calculate the Ratio of Rate of Heat Dissipation (HA/HB):
The rate of heat dissipation, also known as power (H), in a resistor is given by H=P=RV2. Since the conductors are connected in parallel, the potential difference V across them is the same. Therefore, the ratio of heat dissipation rates is:
HBHA=RBV2RAV2=RARBFrom Step 1, we found RB=8RA. Substitute this into the ratio:
HBHA=RA8RA=8So, HBHA=8.
Conclusion:
Based on our calculations:
- vBvA=2
- HBHA=8
Comparing these results with the given options, both vBvA=2 and HBHA=8 are correct.
