Question: Two congruent circles with centre O and O’ intersect at two points A and B. Then \(\angle AOB=\angle...

Question

Two congruent circles with centre O and O’ intersect at two points A and B. Then $\angle AOB=\angle AO'B$ . State true or false.
A. Cannot be decided
B. False
C. True
D. All of the options.

Answer 1

Solution

In this question, we have to find whether the given condition of circles is true or not. Thus, we will use the circles property to get the solution for the problem. As we know, congruent circles are those circles which are the same in size, that have the same radius. We will first draw that figure of two circles, such that they are intersecting each other at point A and B. Then, we will join point OA, OB, O’A, and O’B. Then, we will use the congruence property of the triangle, to prove that the given condition is true, which is the required solution.

Complete step by step solution:
According to the problem, we have to prove the condition of congruent circles.
The condition to be prove is $\angle AOB=\angle AO'B$ ---------- (1)
Now, we will first draw the figure of two circles with center O and O’, such that the circles are intersecting at point A and B. Then, join the lines OA, OB, O’A, AB and O’ B, we get

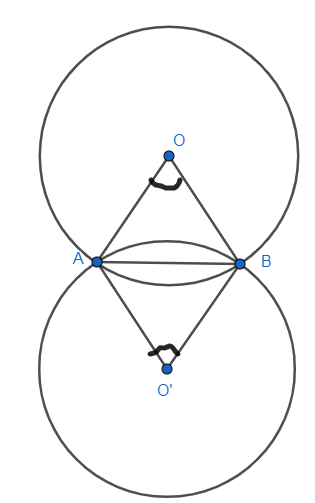
Since, it is given to us that both the circles are congruent to each other, which implies the radius of the both the circles are equal to each other, that is
$OA=OB=O'A=O'B$ --------- (2)
Now, we will use the congruence rule of the circle, that is we will prove that both the triangles are congruent to each other, that is $\Delta AOB\cong \Delta AO'B$ , we get
$OA=O'A$ -------- from equation (2)
$OB=O'B$ -------- from equation (2)
And, $AB=AB$ ----- common side in both the triangles.
Thus, from the above three statements, we get that $\Delta AOB\cong \Delta AO'B$ , by SSS congruence.
Therefore, from the congruent triangles, we get that $\angle AOB=\angle AO'B$ .
Therefore, the given condition $\angle AOB=\angle AO'B$ is true

So, the correct answer is “Option C”.

Note: While solving this problem, do mention the property you are using to avoid confusion and to get the accurate answer. Here, SSS congruence means side-side-side congruence, that is we have proved both the triangle congruent using three sides.