Question
Question: Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is draw...
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP=BQ.
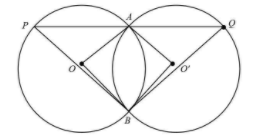
Solution
Here, we will use properties of circles and some properties of rhombus such as (i) Radius of concentric circles is the same and (ii) Opposite angles of a rhombus are equal.
Complete step-by-step solution
Construction:
Join OA, OB, O’A and O’B.
Since OA, OB, O’A and O’B are all radii.
Therefore, OAO’B is a rhombus and the property of rhombus is that opposite angles of a rhombus are equal.
∠AOB=∠AO′B……. (1)
Now, AB is the common chord of the two congruent circles and angle subtended by an arc on the centre is double the angle subtended at any other point on the circle.
∠AOB=2∠APB ∠AOB=2∠AQB…… (2)
From equating the equations (1) and (2).
2∠APB=2∠AQB ∠APB=∠AQB
In triangle PQB, angle ∠APB and angle ∠AQB are equal so sides opposite to these angles that are PB and BQ should also be equal.
Therefore, it is proved that PB=BQ.
Note: Here the circles given are congruent so we can take their radii as equal. In case of similarity, we cannot take radii equal. Make sure to use the property of rhombus i.e “Opposite angles of a rhombus are equal.”
