Question
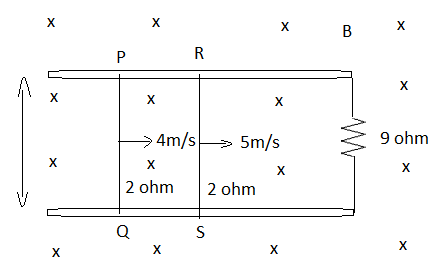
Question: Two conductors PQ and RS are made to slide on the rails with speeds 4m/s and 5m/s respectively in a ...
Two conductors PQ and RS are made to slide on the rails with speeds 4m/s and 5m/s respectively in a region of transverse uniform magnetic field B=1 T as shown in the figure. The electric current in the 9 ohm resistance is
A. 40 mA
B. 45 mA
C. 90 mA
D. 80 mA
Solution
This problem can be solved by the concept of motional emf , which is caused by change in flux. When PQ and RS are moving due to change in area of magnetic field emf is produced and current will flow through the circuit, which will be discussed in the below sections.
Formula used:
ϕ=BA,
Emf E=Blv,
ReqEeq=R1E1+R2E2
Complete Step by step solution:
Magnetic flux depends on three factors: strength of magnetic field, area within the field and orientation of field, change in any of these three factors will lead to change in magnetic flux.
Our problem due to movement of roads is changing continuously and Emf is produced in the circuit.
The flux in a circuit with variable area will be given by ,
ϕ=BA here, ϕ (flux), B (magnitude of magnetic field ) and A (area)
Now, due to movement of rods area is changing continuously so we can change our equation to,
⇒ϕ=Blx
Now by faraday's law, change in magnetic flux will leads to induced emf in a circuit so,
⇒E=dtdϕ
⇒E=Bldtdx=Blv
Now, given in the question, B=1, l=10cm=0.1m, vPQ=4m/sand vRS=5m/s.
So, induced emf in PQ is E1=1×0.1×4=52,
Induced emf in RS is E2=1×0.1×5=21
Now, we know that equivalent voltage across parallel combination is given by,
ReqEeq=R1E1+R2E2, here R1andR2 are resistance of PQ and RS, and this equation will also gives total current flowing the circuit so,
⇒ReqEeq=22/5+21/2
⇒ReqEeq=21(105+4)
⇒ReqEeq=209=0.45=45mA
So, due to change in flux and induced emf in the circuit the current flowing through 9Ω resistance is equal to 45mA.
Hence, option (B) is correct.
Note:
The calculation of motional emf is not only limited to rods, because of Faraday's law we can see that change in magnetic flux caused by any conductor with motion can induce emf in a circuit. So this law holds for all flux changes either due to change in magnetic field or due to motion of conductor.
