Question

Two conducting spheres of radii $R_{1}$ and $R_{2}$ carrying uniform volume charge densities $+\rho$ and $-\rho$, respectively, are placed such that they partially overlap, as shown in the figure. At all points in the overlapping region:(this question has multiple correct options)

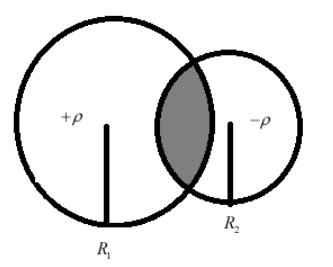
A. the electrostatic field is zero
B. the electrostatic potential is constant
C. the electrostatic field is constant in magnitude
D. the electrostatic field has same direction

Answer 1

Electric field is the electric force due to a unit charge positive charge which is at rest exerted on its surrounding. We can find the electric field due to the individual charges and then sum them to find the electric field at the shaded region.
Formula: $E=\dfrac{F}{q}$or$E=\dfrac{kq}{r^{2}}$

Complete answer:
We know that the electric force due to a pair of charges is given by Coulomb's law. An electric field can be produced by a time-varying electric field or an electrical charge. These can be either attracting or repelling in nature.
An electric field E is defined as the electric force F per unit positive charge q, which is infinitesimally small and at rest, and is given as $E=\dfrac{F}{q}$. Then$E=\dfrac{kq}{r^{2}}$, where $k=\dfrac{1}{4\pi\epsilon_{0}}$ which is a constant and $r$ is the distance between the unit charges. Since the electric field is a vector quantity, it acts along the direction of the distance $r$, then we can denote it as $\vec E=\dfrac{kq\vec r}{r^{3}}$.
Here, we have two spheres, let $+\rho$ be the volume density of the sphere $R_{1}$ and, let $-\rho$ be the volume density of the sphere $R_{2}$. Let the distance between the two radii be $d$.Then the charge $q_{1}$ on $R_{1}$ is given as $+\rho\dfrac{4}{3}\pi R_{1}^{3}$ and the charge $q_{2}$ on $R_{2}$ is given as $-\rho\dfrac{4}{3}\pi R_{2}^{3}$. If $P$ is point in the shaded region, let us assume that it is at a distance $r_{1}$ and $r_{2}$ from the radii $R_{1}$ and $R_{2}$ respectively.
Then, consider the figure shown, below.

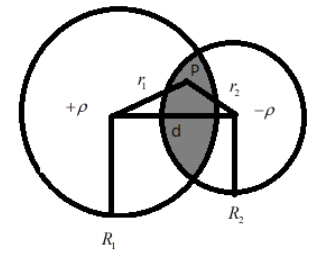
Cleary, the electric field at $P$ is the superposition of the electric field vectors due to $R_{1}$ and $R_{2}$, it is given as $E_{P}=\dfrac{K\left(+\rho\dfrac{4}{3}\pi R_{1}^{3}\right)\vec r_{1}}{R_{1}^{3}}+\dfrac{K\left(-\rho\dfrac{4}{3}\pi R_{2}^{3}\right)\vec r_{2}}{ R_{2}^{3}}=K\rho\dfrac{4}{3}\pi(\vec r_{1}-\vec r_{2})$
From the triangle in the figure, we can say that, $d=r_{1}-r_{2}$ due to the vector addition .
Then, $E_{P}=K\rho\dfrac{4}{3}\pi \vec d$
Thus, we can say that the direction of the electric field is unchanged, i.e from positive to negative.

Thus the answer is D. the electrostatic field has same direction

Note:
Electric field is in the direction of the force. Usually, the electric field of a point positive charge is radially outwards, whereas the electric field of a point negative charge is radially inwards to the charge. However, the electric field also depends on the symmetry of the charge carrying conductor.