Question

Two conducting circular loops of radii ${R_1}$ and ${R_2}$ $\left( {{R_1} > > {R_2}} \right)$ are placed in the same plane with their centers coinciding. Find the mutual inductance between them.
(A) $\dfrac{{{\mu _0}\pi R_1^2}}{{{R_2}}}$
(B) $\dfrac{{{\mu _0}\pi R_2^2}}{{{R_1}}}$
(C) $\dfrac{{{\mu _0}\pi R_1^2}}{{2{R_2}}}$
(D) $\dfrac{{{\mu _0}\pi R_2^2}}{{2{R_1}}}$

Answer 1

Hint : To solve this question, we have to assume a particular value of current flowing in the circular loop of large radius. Then we have to find the magnetic flux linked in the circular loop of small radius, from which we can get the required value of the mutual inductance.

Formula used: The formulae which have been used to solve this question are given by
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{2{R_1}}}$ , here $B$ is the magnetic field at the centre of a circular coil of radius $R$ due to a current of $I$ flowing through it.
$\Rightarrow \varphi = {\rm M}{\rm I}$ , here $\varphi$ is the flux linkage, $M$ is the mutual inductance, and $I$ is the current.

Complete step by step answer
Let the mutual inductance between the two loops be $M$ .
Let us represent the situation given by the figure below.

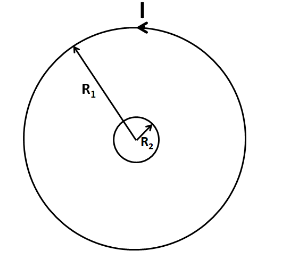
Let us assume that a current of $I$ is flowing in the bigger circular loop. Due to this current in the bigger loop, there will be a magnetic field set up at its centre. This magnetic field is given by
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{2{R_1}}}$ ……………………..(1)
According to the question, ${R_1} > > {R_2}$ , that is, the radius of the smaller loop is negligible as compared to that of the bigger loop. As both the loops are placed with their centers coinciding, so the whole area of the smaller loop can be assumed to be placed at the centre of the bigger loop. So the magnetic field within the region of the circular loop can be approximated to that produced by the bigger loop at its centre. So the magnetic flux linked with the smaller loop is given by
$\Rightarrow \varphi = {\rm B}{\rm A}$
We know that the area of the circular loop is $A = \pi R_2^2$ . Also from (1) we have $B = \dfrac{{{\mu _0}I}}{{2{R_1}}}$ . Substituting these above, we get the flux linkage as
$\Rightarrow \varphi = \dfrac{{{\mu _0}I\pi R_2^2}}{{2{R_1}}}$ ……………………..(2)
Now, we know that the flux linkage can also be written as
$\Rightarrow \varphi = {\rm M}{\rm I}$ …………………….(3)
Equating (2) and (3) we have
$\Rightarrow {\rm M}{\rm I} = \dfrac{{{\mu _0}I\pi R_2^2}}{{2{R_1}}}$
Finally, on cancelling $I$ from both the sides, we get
$\Rightarrow {\rm M} = \dfrac{{{\mu _0}\pi R_2^2}}{{2{R_1}}}$.

Note
The mutual inductance discussed in this question is the basic principle for the operation of electric devices such as transformers, electric motors, generators etc. These all have coils which interact with the magnetic field produced by the other coils.