Question

Two conducting and concentric thin spherical shells of radii $a$ and $b$,$(b > a)$ have charges ${q_1}$ and ${q_2}$ ​ respectively. Now if the inner shell is earthed then the final charge on this shell will be
(a) $\dfrac{{{q_2}{a^2}}}{{{b^2}}}$
(b) $\dfrac{{ - {q_2}a}}{b}$
(c) $\dfrac{{({q_1} - {q_2})}}{2}$
(d) $- \dfrac{{{q_2}b}}{a}$

Answer 1

they have given the two thin conducting and concentric shell of radii $a$ and $b$,$(b > a)$ now here we have to find the final charge on the given shell if the inner shell is earthed first we have to draw a diagram as per my knowledge it is just like gauss law which one of the fundamental Maxwell's equation which describes the relation of the electric field on a Gaussian surface and the total charge enclosed in it.

Complete step by Step solution:

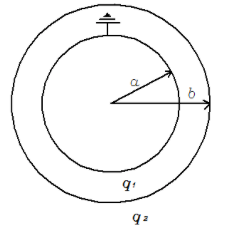
The inner conducting and concentric thin spherical shell is grounded
Therefore the potential $V$ will be $0$
Also the potential at the inner spherical is given by
$V = \dfrac{{K{Q_1}}}{a} + \dfrac{{K{Q_2}}}{b}$
In the earlier as we taken the potential $V$ will be $0$ that is $V = 0$ substitute it in the above equation
$0 = \dfrac{{K{Q_1}}}{a} + \dfrac{{K{Q_2}}}{b}$
Here in the above equation we can see that $K$ is constant so take it outside
Then the equation can be written as
$0 = K\left( {\dfrac{{{Q_1}}}{a} + \dfrac{{{Q_2}}}{b}} \right)$
Here $K$ is a constant so its value will be $1$then
$0 = \left( {\dfrac{{{Q_1}}}{a} + \dfrac{{{Q_2}}}{b}} \right)$
Now we want the value of ${Q_1}$so take the whole term outside then the equation will be
$- \dfrac{{{Q_1}}}{a} = \dfrac{{{Q_2}}}{b}$
Now we want only the value of ${Q_1}$ so shift $a$ to the R.H.S then we get
$- {Q_1} = \dfrac{{{Q_2}a}}{b}$
Therefore ${Q_1} = - \dfrac{{{Q_2}a}}{b}$
Therefore the final charge on this shell ${Q_1} = - \dfrac{{{Q_2}a}}{b}$

Hence the correct answer is option (d)

Note: Electric potential is the amount of work needed to move a unit charge from a source point to a particular point against an electric field. Typically, the source point is Earth, although any point beyond the influence of the electric field charge can be used.