Question

Two condensers, one of capacity $C$ and another of capacity $\dfrac{C}{2}$ are connected to a $V$ volt battery, as shown.

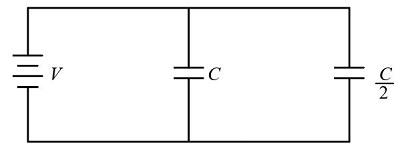
The work done by battery in charging fully both the condensers is:-
(A) $\dfrac{1}{2}C{V^2}$
(B) $2C{V^2} (C)$\dfrac{1}{4}C{V^2}$(D)$\dfrac{3}{4}C{V^2}$

Answer 1

Here, in this question both the capacitors are connected in parallel with each other. Then, the potential difference across both the condensers remains as it was before. Then, we will apply the formula for charge on the condenser. Then, we use the formula to find the work done or the energy stored in the capacitor.

Complete step by step answer:
Given: The capacity of two conductors are $C$ and $\dfrac{C}{2}$ accordingly. The conductors are connected to a battery of $V\;{\rm{volt}}$.

First, we write the formula for charge on the capacitor $C$,
${q_1} = CV$
Here, ${q_1}$ is the charge on the first capacitor of capacity $C$.
Now, we write the charge on the second capacitor of capacity $\dfrac{C}{2}$,
$\begin{array}{l} {q_2} = \dfrac{C}{2}V\\\ \Rightarrow {q_2} = \dfrac{{CV}}{2} \end{array}$
Here, ${q_2}$ is the charge on the second capacitor.
We write the formula to find the equivalent charge in the parallel,
$q = {q_1} + {q_2}$
Now, substitute the values of charges for both the conductors in above relation.
$q = CV + \dfrac{{CV}}{2}$
Now, we perform the addition of both the given charges,
$\begin{array}{l} q = \dfrac{{2CV + CV}}{2}\\\ \Rightarrow q = \dfrac{3}{2}CV \end{array}$

Now, we apply the formula to find the work done in fully charging of both the conductors,
$w = \dfrac{1}{2}qV$
We substitute the obtained value of equivalent charge in above relation,
$\begin{array}{l} w = \dfrac{1}{2} \times \dfrac{3}{2}CV \times V\\\ \Rightarrow w = \dfrac{3}{4}C{V^2} \end{array}$
Therefore, the work done in fully charging both the conductors is $\dfrac{3}{4}C{V^2}$.

So, the correct answer is “Option D”.

Note:
The capacitors are said to be connected in parallel if both of the terminals of the capacitor are connected to each terminal of another capacitor. The formula for parallel connected conductors helps in many cases to calculate the resistance of a complex circuit that consists of many resistors.