Question

Two concentric thin metallic spheres of radii ${R_1}$ and ${R_2}$ $\left( {{R_1} > {R_2}} \right)$ bear charges ${Q_1}$ and ${Q_2}$ respectively. Then the potential at a radius $r$ between ${R_1}$ and ${R_2}$ will be $1/4(\pi {\varepsilon _0})$ times:
(A) $\dfrac{{{Q_1} + {Q_2}}}{4}$
(B) $\dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{r}$
(C) $\dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{{{R_2}}}$
(D) $\dfrac{{{Q_1}}}{{{R_2}}} + \dfrac{{{Q_2}}}{{{R_1}}}$

Answer 1

We consider two concentric thin metallic spheres of radii ${R_1}$ containing a charge ${Q_1}$ and ${R_2}$ containing a charge ${Q_2}$ . We are considering a particular radius $r$ that is located between the radii of the two spheres. We have to find the potential at this particular radius.

Complete Step by step solution:
There will be potential due to the two charged spheres.
The radius $r$ will be inside the sphere of radius ${R_1}$ and outside the sphere of radius ${R_2}$ as shown in the figure.

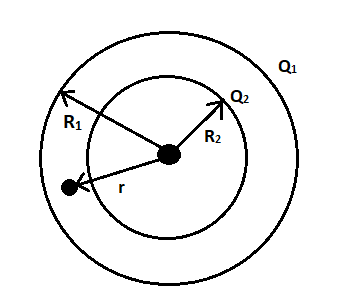
Let the potential due to the sphere of radius ${R_2}$ be ${V_2} = k\dfrac{{{Q_2}}}{r}$ since $r$ is outside the sphere
Let the potential due to the sphere of radius ${R_1}$ be ${V_1} = k\dfrac{{{Q_1}}}{{{R_1}}}$ as the radius $r$ is inside the sphere the potential will be constant.
The total potential at the radius $r$ can be written as,
${V_r} = {V_1} + {V_2}$
Substituting the values of ${V_1}$ and ${V_2}$ within the above equation, we get
${V_r} = k\dfrac{{{Q_2}}}{r} + k\dfrac{{{Q_1}}}{{{R_1}}}$
Taking the common term $k$ outside, we get
${V_r} = k\left( {\dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{r}} \right)$
It is given that $k = 1/4(\pi {\varepsilon _0})$
The answer is: Option (B): $\dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{r}$ .

Additional Information
Surfaces having the same potential at every point is called equipotential surfaces. The electric field is usually normal to the equipotential surface. For moving a charge on the equipotential surface no work is required.

Note:
There is a potential associated with every field. The potential associated with an electric field is called electric potential. It is a scalar quantity. The electric field to some extent is the negative gradient of the electrical potential at that point. It is the work done in bringing a positive charge $q\;$ from infinity to that point. The potential decreases within the direction of the electrical field.