Question

Two concentric, thin metallic spheres of radii ${R_1}$ and ${R_2}$ ( ${R_1} > {R_2}$ ) bear charges ${Q_1}$ and ${Q_2}$ respectively. Then the potential at distance $r$ between ${R_1}$ and ${R_2}$ will be $\left( {k = \dfrac{1}{{4\pi {\varepsilon _0}}}} \right)$
(A) $k\left( {\dfrac{{{Q_1} + {Q_2}}}{r}} \right)$
(B) $k\left( {\dfrac{{{Q_1}}}{r} + \dfrac{{{Q_2}}}{{{R_2}}}} \right)$
(C) $k\left( {\dfrac{{{Q_2}}}{r} + \dfrac{{{Q_1}}}{{{R_1}}}} \right)$
(D) $k\left( {\dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{{{R_2}}}} \right)$

Answer 1

We are asked to find the potential at a point given. For this, you can start by drawing a suitable diagram according to the question. Then we find the potential due to each of the spheres individually and add them. This will lead us to the right answer.
The formula used to find the potential at any point is given by, $V = k\dfrac{Q}{r}$
Where $\left( {k = \dfrac{1}{{4\pi {\varepsilon _0}}}} \right)$
$Q$ is the charge due to which the potential is to be found
$r$ is the distance of the point from the charge.

Complete answer:
Let us start by drawing the diagram according to the question.

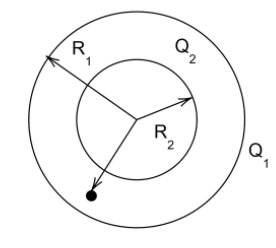
Electric potential is defined as the amount of work needed to move a unit charge from a reference point to a specific point against an electric field.
Now that we have defined what electric potential is, we can move onto finding the potential due to the two concentric circles at a given point. We do this by adding the values of potential due to the two circles individually.
The potential can be found using the formula, $V = k\dfrac{Q}{r}$
The potential due to sphere of radius ${R_1}$ is ${V_1} = k\dfrac{{{Q_1}}}{{{R_1}}}$
The potential due to sphere of radius ${R_2}$ is ${V_2} = k\dfrac{{{Q_2}}}{r}$
As we said earlier, we add these values to get the total potential
$V = {V_1} + {V_2} = k\dfrac{{{Q_1}}}{{{R_1}}} + k\dfrac{{{Q_2}}}{r} = k\left( {\dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{r}} \right)$
In conclusion, the right answer is option (C) $k\left( {\dfrac{{{Q_2}}}{r} + \dfrac{{{Q_1}}}{{{R_1}}}} \right)$ .

Note:
While electric potential energy has a dependency upon the charge of the object experiencing the electric field, electric potential is purely location dependent. Electric potential is the potential energy per charge. As you do work on a charge to move it closer to another charge of the same sign, you increase the electric potential energy. That's because like charges repel each other, so it takes more and more energy to move the charges together the closer you get.