Question

Two concentric spherical shells of radii a and 1.2a have charges +Q and -2Q respectively. At what distance from centre potential will be the same as that of centre?
a) 2a
b) 1.5a
c) 2.5a
d) 3a

Answer 1

The potential at the centre will be the sum of potential due to the two the individual concentric shells. This is because we can break the charge on the either shells infinitesimally so small such that the potential due to the individual charge at the centre from radius r is $V=\dfrac{kq}{r}$ here k is the permittivity of free space. If we see the equation k and r are constants. But the charge q is just an individual charge but on a shell there will be N number of charges and the sum of potential of each of them will give the total potential at the centre. Further we can take a general expression of potential by both the shells at some distance d and equate it to the centre potential and get the required answer.

Complete step-by-step answer:

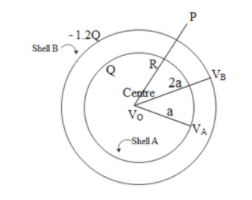
From the above diagram we can see that the potential on the shell of radius a is denoted by ${{V}_{A}}$ and potential on the shell at radius 1.2a from the centre is denoted by ${{V}_{B}}$ . Hence potential at the centre is given by, ${{\text{V}}_{\text{O}}}\text{=}{{\text{V}}_{\text{A}}}\text{+}{{\text{V}}_{\text{B}}}\text{where}{{\text{V}}_{\text{A}}}\text{ and }{{\text{V}}_{\text{B}}}\text{ are the potentials on their individual surfaces}\text{.}$
Hence,
${{V}_{O}}=\dfrac{kQ}{a}+\dfrac{-k2Q}{1.2a}=\dfrac{kQ}{a}\left( \dfrac{12-20}{12} \right)=\dfrac{2}{3}\dfrac{kQ}{a}...(1)$
where k is the permittivity of free space.

Now we wish to calculate the potential at a point such that its value of potential is the same as that of the centre. Let that point be P at a distance r from the centre.

Hence potential at point P is given by i.e. ${{\text{V}}_{\text{P}}}$ ,
${{\text{V}}_{\text{P}}}\text{=Potential due to shell A+Potential due to shell B}$
${{\text{V}}_{\text{P}}}\text{=}\dfrac{\text{kQ}}{R}\text{+}\dfrac{k(-2Q)}{R}=\dfrac{\text{kQ}}{R}\left( 1-2 \right)=-\dfrac{\text{kQ}}{R}...(2)$

Equating equation 1 by two we get,
$\dfrac{\text{kQ}}{R}=\dfrac{2}{3}\dfrac{\text{k}Q}{a}\text{, hence R}=\dfrac{3}{2}a=1.5a$

So, the correct answer is “Option b”.

Note: It is to be noted that That the potential on the either shells is equal to the potential at the centre. However the electric field inside the shell A is zero. But the field inside the shell B is completely not zero due to the field between the negative and the positive nature of the either shells.