Question

Two concentric spheres of radii $\mathrm{R}$ and $\mathrm{r}$ have positive charges $\mathrm{q}_{1}$ and $\mathrm{q}_{2}$ with equal surface charge densities. What is the electric potential at their common centre?
A) $\dfrac{\sigma}{\varepsilon_{0}}(\mathrm{R}+\mathrm{r})$
B) $\dfrac{\sigma}{\varepsilon_{0}}(\mathrm{R}-\mathrm{r})$
C) $\dfrac{\sigma}{\varepsilon_{0}}\left(\dfrac{1}{\mathrm{R}}+\dfrac{1}{\mathrm{r}}\right)$
D) $\dfrac{\sigma}{\varepsilon_{0}}\left(\dfrac{\mathrm{R}}{\mathrm{r}}\right)$

Answer 1

We know that by surface charge density we mean the amount of electric charge that is present on the surface. The unit to measure this is charge per unit area. The volume and the surface area of the concerned surface is taken into consideration. For this question, the surface area of the sphere is required.

Complete step by step answer:
Let us draw the diagram, for a better understanding.

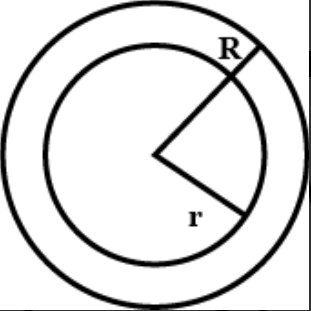
Let us consider that the radius of the outer sphere is R and the radius of the inner sphere is r. Thus, we can write that:
Charge on the outer sphere, $\mathrm{q}_{1}=4 \pi \mathrm{R}^{2} \sigma$ and,
Charge on the inner sphere, $\mathrm{q}_{2}=4 \pi \mathrm{r}^{2} \sigma$
Now let us consider that the electric potential is defined as v. So, the electric potential of the common centre will be given as the summation of the charges on both the outer and the inner spheres.
Hence, we can write that:
$\Rightarrow \mathrm{v}=\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{\mathrm{q}_{1}}{\mathrm{R}}+\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{\mathrm{q}_{2}}{\mathrm{r}}$
After the summation we get the value of v as:
$\Rightarrow \dfrac{1}{4 \pi \varepsilon_{0}}\left[\dfrac{4 \pi \mathrm{R}^{2} \sigma}{\mathrm{R}}+\dfrac{4 \pi \mathrm{r}^{2} \sigma}{\mathrm{r}}\right]$
$\Rightarrow \dfrac{4 \pi \sigma}{4 \pi \varepsilon_{0}}(\mathrm{R}+\mathrm{r})$
$\Rightarrow \dfrac{\sigma}{\varepsilon_{0}}(\mathrm{R}+\mathrm{r})$
Thus, the electric potential is: $\dfrac{\sigma}{\varepsilon_{0}}(\mathrm{R}+\mathrm{r})$.

Hence, the correct option is Option A.

Note: Electric potential gives us an idea about the amount of work that is required to be done in order to remove a unit of electric charge from a point to another specific point in the electric field. Thus, the total work that will be done by the external agent will give us an idea about the electric potential. The SI unit of electric potential is considered to be Volts. The main purpose of finding the electric potential is to get an idea about the source of the electric field on the basis of the location of the point that is present within the electric field. As because the electric potential is derived from the energy of the external agent it will be considered as a scalar quantity.