Solveeit Logo
Login

Question

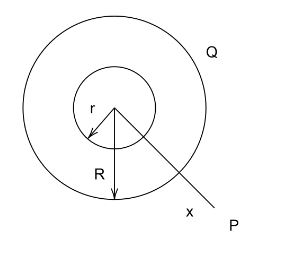
Question: Two concentric hollow conducting spheres of radius \(r\) and \(R\) are shown. The charge on the oute...

Two concentric hollow conducting spheres of radius rr and RR are shown. The charge on the outer shell is QQ. What charge should be given to the inner sphere so that potential at any point PP outside the outer sphere is zero?
A. −QrR\dfrac{{ - Qr}}{R}
B. −QRr\dfrac{{ - QR}}{r}
C. −Q - Q
D. −2QRr\dfrac{{ - 2QR}}{r}

Explanation

Solution

We are given two concentric circles of radius r and R. We are asked to find the charge on the smaller circle if the potential outside the shell is zero. We can start to answer this question by writing down the values given in the question. We can then move onto finding the required solution. We can do this by using the value of total potential and equate it to zero and find the value of potential in the inner circle. This will lead us to the required solution.

Formulas used:
The potential outside the circles can be found using
V=Q4πε0R+q4πε0RV = \dfrac{Q}{{4\pi {\varepsilon _0}R}} + \dfrac{q}{{4\pi {\varepsilon _0}R}}
Where qq is the charge of the smaller circle.

Complete step by step answer:
We are given that, for the circle of radius R, the charge is Q. Potential can be defined as the work done to bring a charge from a reference point to a particular point. We can find the value of charge in the inner circle by using the formula,
V=Q4πε0R+q4πε0RV = \dfrac{Q}{{4\pi {\varepsilon _0}R}} + \dfrac{q}{{4\pi {\varepsilon _0}R}}

When we equate it to zero, we get

\Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}R}} \times \left( {Q + q} \right) = 0$$ We take the constant to the other side and get $$Q + q = 0 \\\ \therefore q = - Q$$ This gives us the value of charge on the inner circle to be negative of the charge on the outer circle. **Hence, the correct answer is C.** **Note:** We can see that the value of total potential is taken as $$V = \dfrac{Q}{{4\pi {\varepsilon _0}R}} + \dfrac{q}{{4\pi {\varepsilon _0}R}}$$. The value of distance is taken as R in both the cases. This is done because the radius of the bigger circle is considered in this type of problem. That is because the charges in both the circles behave as point charges.