Solveeit Logo
Login

Question

Question: Two concentric conducting spherical shells of radii \(a_1\) and \(a_2\) (\(a_2\) > \(a_1\) ) are cha...

Two concentric conducting spherical shells of radii a1a_1 and a2a_2 (a2a_2 > a1a_1 ) are charged to potentials ϕ1{\phi _1} and ϕ2{\phi _2}, respectively. Find the charge on the inner shell.
A. 4π∈0(ϕ1−ϕ2a2−a1)a1a2 B. 4π∈0(ϕ1+ϕ2a2+a1)a1a2 C. π∈0(ϕ1−ϕ2a2+a1)a1a2 D. 2π∈0(ϕ1+ϕ2a2−a1)a1a2  {\text{A}}{\text{. 4}}\pi { \in _0}(\dfrac{{{\phi _1} - {\phi _2}}}{{{a_2} - {a_1}}}){a_1}{a_2} \\\ {\text{B}}{\text{. 4}}\pi { \in _0}(\dfrac{{{\phi _1} + {\phi _2}}}{{{a_2} + {a_1}}}){a_1}{a_2} \\\ {\text{C}}{\text{. }}\pi { \in _0}(\dfrac{{{\phi _1} - {\phi _2}}}{{{a_2} + {a_1}}}){a_1}{a_2} \\\ {\text{D}}{\text{. 2}}\pi { \in _0}(\dfrac{{{\phi _1} + {\phi _2}}}{{{a_2} - {a_1}}}){a_1}{a_2} \\\

Explanation

Solution

- Hint: The potential present on any spherical body of charge q and radius will be: Kqr\dfrac{{Kq}}{r} where K=14π∈0K = \dfrac{1}{{4\pi { \in _0}}} . one thing must be cared here is when we are writing potential of outer sphere then either charge is on the outer sphere or inner sphere radius will always be written of outer sphere but when we are writing potential of inner sphere then for charge on inner sphere its radius is written and for charge charge of outer sphere its own radius will be written.

Formula used:
The potential present on any spherical body of charge q and radius will be: Kqr\dfrac{{Kq}}{r} where K=14π∈0K = \dfrac{1}{{4\pi { \in _0}}}

Complete step-by-step answer:

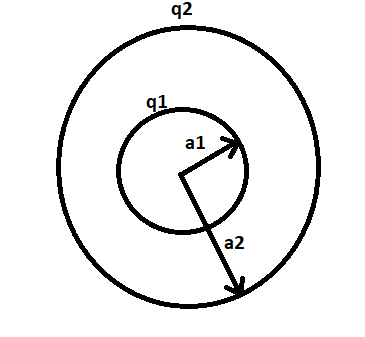
Calculate the value of potential on the outer sphere.
ϕ2=kq1a2+kq2a2{\phi _2} = \dfrac{{k{q_1}}}{{{a_2}}} + \dfrac{{k{q_2}}}{{{a_2}}}
Potential on the inner sphere:
ϕ1=kq1a1+kq2a2{\phi _1} = \dfrac{{k{q_1}}}{{{a_1}}} + \dfrac{{k{q_2}}}{{{a_2}}}
Subtract ϕ2{\phi _2} from ϕ1{\phi _1}.
ϕ1−ϕ2=kq1a1−kq1a2 ϕ1−ϕ2=Kq1(1a1−1a2) ϕ1−ϕ2=Kq1(a2−a1a1a2) q1=(ϕ1−ϕ2a2−a1)a1a2K K=14π∈0 q1=4π∈0(ϕ1−ϕ2a2−a1)a1a2 {\phi _1} - {\phi _2} = \dfrac{{k{q_1}}}{{{a_1}}} - \dfrac{{k{q_1}}}{{{a_2}}} \\\ {\phi _1} - {\phi _2} = K{q_1}(\dfrac{1}{{{a_1}}} - \dfrac{1}{{{a_2}}}) \\\ {\phi _1} - {\phi _2} = K{q_1}(\dfrac{{{a_2} - {a_1}}}{{{a_1}{a_2}}}) \\\ {q_1} = (\dfrac{{{\phi _1} - {\phi _2}}}{{{a_2} - {a_1}}})\dfrac{{{a_1}{a_2}}}{K} \\\ K = \dfrac{1}{{4\pi { \in _0}}} \\\ {q_1} = 4\pi { \in _0}(\dfrac{{{\phi _1} - {\phi _2}}}{{{a_2} - {a_1}}}){a_1}{a_2} \\\
The correct option is (A).

Note: Whenever we get this type of question the key concept of solving is we have to be conceptually clear about the writing potential of the sphere and also have knowledge of charge distribution of the sphere when any sphere is earthed. Also remember when any sphere is earthed its potential becomes 0 not its charge.