Solveeit Logo
Login

Question

Question: Two concentric coils each of radius equal to \(2\pi cm\) are placed at right angles to each other. I...

Two concentric coils each of radius equal to 2πcm2\pi cm are placed at right angles to each other. If 3A and 4A are the currents flowing through the two coils respectively, the magnetic induction (in Wbm−2Wb{{m}^{-2}}) at the centre of the coils will be
A. 12×10−512\times {{10}^{-5}}
B. 10−5{{10}^{-5}}
C. 5×10−55\times {{10}^{-5}}
D. 7×10−57\times {{10}^{-5}}

Explanation

Solution

We are given two concentric coils placed at right angles with each other which implies that the axis of both the coils and thus their respective magnetic fields must also be perpendicular to each other. Therefore, we shall find the magnetic fields due to both the coils individually and then find their resultant net value of magnetic induction at their centre.

Complete step by step solution:
The magnetic field, BB due to a circular coil is given as:
B=μ0i2rB=\dfrac{{{\mu }_{0}}i}{2r}
Where,
μ0={{\mu }_{0}}= magnetic permeability constant and μ0=4π×10−7 WbA−1m−1{{\mu }_{0}}=4\pi \times {{10}^{-7}}\,Wb{{A}^{-1}}{{m}^{-1}}
i=i= current in the coil
r=r= radius of coil

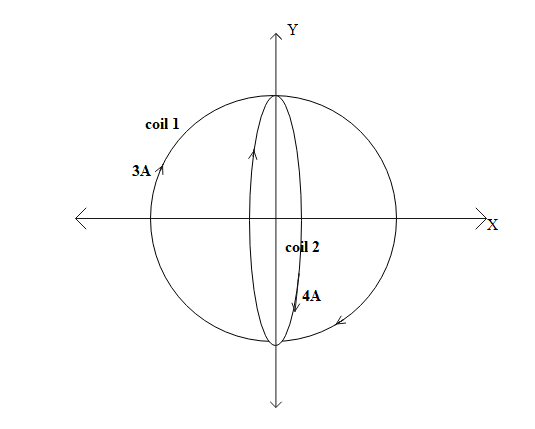
For coil 1, we have i=3Ai=3A and r=2πcmr=2\pi cm or r=2π×10−2mr=2\pi \times {{10}^{-2}}m,
Applying the above formula of magnetic field, we get
B1=μ0(3)2(2π×10−2){{B}_{1}}=\dfrac{{{\mu }_{0}}\left( 3 \right)}{2\left( 2\pi \times {{10}^{-2}} \right)}
Now, we shall put the value the magnetic permeability constant and then we get,
⇒B1=(4π×10−7)(3)2(2π×10−2)\Rightarrow {{B}_{1}}=\dfrac{\left( 4\pi \times {{10}^{-7}} \right)\left( 3 \right)}{2\left( 2\pi \times {{10}^{-2}} \right)}
Here, we cancel 4π4\pi and 10−2{{10}^{-2}} from the numerator and denominator.
⇒B1=3×10−5\Rightarrow {{B}_{1}}=3\times {{10}^{-5}} ……………….. (1)
Similarly, for coil 2, we have i=4Ai=4A and r=2πcmr=2\pi cm or r=2π×10−2mr=2\pi \times {{10}^{-2}}m,
Applying the above formula of magnetic field, we get
B2=μ0(4)2(2π×10−2){{B}_{2}}=\dfrac{{{\mu }_{0}}\left( 4 \right)}{2\left( 2\pi \times {{10}^{-2}} \right)}
Now, we shall put the value the magnetic permeability constant and then we get,
⇒B2=(4π×10−7)(4)2(2π×10−2)\Rightarrow {{B}_{2}}=\dfrac{\left( 4\pi \times {{10}^{-7}} \right)\left( 4 \right)}{2\left( 2\pi \times {{10}^{-2}} \right)}
Here, we cancel 4π4\pi and 10−2{{10}^{-2}} from the numerator and denominator.
⇒B2=4×10−5\Rightarrow {{B}_{2}}=4\times {{10}^{-5}} ………………. (2)
Now, we find the resultant net magnetic field using the formula B=B12+B22B=\sqrt{B_{1}^{2}+B_{2}^{2}}.
Substituting the values of B1{{B}_{1}} and B2{{B}_{2}} from (1) and (2), we get
⇒B=(3×10−5)2+(4×10−5)2\Rightarrow B=\sqrt{{{\left( 3\times {{10}^{-5}} \right)}^{2}}+{{\left( 4\times {{10}^{-5}} \right)}^{2}}}
Taking (10−5)2{{\left( {{10}^{-5}} \right)}^{2}} common and finding their square, we get

& \Rightarrow B=\sqrt{{{\left( {{10}^{-5}} \right)}^{2}}\left( {{3}^{2}}+{{4}^{2}} \right)} \\\ & \Rightarrow B={{10}^{-5}}\sqrt{{{3}^{2}}+{{4}^{2}}} \\\ \end{aligned}$$ We know that ${{3}^{2}}=3\times 3=9$ and $${{4}^{2}}=4\times 4=16$$. Thus, substituting these values and solving further. $\begin{aligned} & \Rightarrow B={{10}^{-5}}\sqrt{9+16} \\\ & \Rightarrow B={{10}^{-5}}\sqrt{25} \\\ & \Rightarrow B=5\times {{10}^{-5}} \\\ \end{aligned}$ Therefore, the magnetic induction at centre is $5\times {{10}^{-5}}Wb{{m}^{-2}}$. **Hence, the correct option is (C) $5\times {{10}^{-5}}$.** **Note:** The magnetic field is a vector quantity which has both magnitude and direction. Thus, the resultant of two or more magnetic field values is calculated by using rules of vector addition. Since, most of the quantities that we deal with in physics are vectors, therefore, one must have appropriate knowledge of vectors beforehand only.