Solveeit Logo
Login

Question

Question: Two concentric coils, each of radius equal to \(2\pi \) cm, are placed at right angles to each other...

Two concentric coils, each of radius equal to 2π2\pi cm, are placed at right angles to each other. Currents of 3A and 4A, respectively, are flowing through two coils. The magnetic Induction, in Wbm−2,Wb{m^{ - 2}}, at the center of the coils will be μ0=4π×10−7Wb(Am−1){\mu _0} = 4\pi \times {10^{ - 7}}Wb\left( {A{m^{ - 1}}} \right)
A. 5×10−55 \times {10^{ - 5}}
B. 7×10−57 \times {10^{ - 5}}
C. 12×10−512 \times {10^{ - 5}}
D. 1×10−5{\kern 1pt} 1 \times {10^{ - 5}}

Explanation

Solution

Hint: The magnetic field lines are concentric circles at every point of a current carrying circular loop. Through the right-hand thumb rule one will find the position of the magnetic field of each segment of the circular loop.

Complete step-by-step answer:


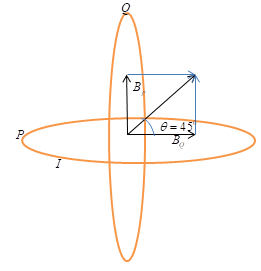
In the above figure since coils P and Q have the common center.
Bp{B_p} is directed vertically upward and BQ{B_Q} is directed horizontally
Therefore the resultant magnetic field is given by,
BR=BP2+BQ2{B_R} = \sqrt {B_P^2 + B_Q^2}
Now let calculate the magnetic field due to the coil Bp{B_p}
Bp=μ0i2r=μ0iP2(2π×10−2)=μ0×3×1024π{B_p} = \dfrac{{{\mu _0}i}}{{2r}} = \dfrac{{{\mu _0}{i_P}}}{{2\left( {2\pi \times {{10}^{ - 2}}} \right)}} = \dfrac{{{\mu _0} \times 3 \times {{10}^2}}}{{4\pi }}
Now magnetic field due to the coil BQ{B_Q}
BQ=μ0i2r=μ0iQ2(2π×10−2)=μ0×4×1024π{B_Q} = \dfrac{{{\mu _0}i}}{{2r}} = \dfrac{{{\mu _0}{i_Q}}}{{2\left( {2\pi \times {{10}^{ - 2}}} \right)}} = \dfrac{{{\mu _0} \times 4 \times {{10}^2}}}{{4\pi }}
Now the resultant magnetic field is given by
BR=BP2+BQ2=μ04π×0.5×102 BR=10−7×5×102 BR=5×10−5Wb/m2  {B_R} = \sqrt {B_P^2 + B_Q^2} = \dfrac{{{\mu _0}}}{{4\pi }} \times 0.5 \times {10^2} \\\ {B_R} = {10^{ - 7}} \times 5 \times {10^2} \\\ {B_R} = 5 \times {10^{ - 5}}Wb/{m^2} \\\
Hence, the correct option is “A”.
Additional Information- At either point of a current bearing circular coil , the magnetic field lines are concentrated loops. Through the right-hand thumb rule one will find the position of the magnetic field of each segment of the circular loop. The magnetic field lines are straight in the middle of the circular coil.

Note - At the center of the circular loop, The magnetic field lines are straight. Each part of the ring loop produced in the same direction magnetic field lines with the ring loop. The magnetic field direction is perpendicular to the spinal position at the Center of the circular coil or around the coil axis.