Question

Two concentric coils each of radius equal to 2$\pi$cm are placed at right angles to each other. 3 ampere and 4 ampere are the currents flowing in each coil respectively. The magnetic induction in $weber/{m^2}$ at the center of coils will be ($\mu = 4\pi \times {10^{ - 7}}Wb/A.m$)
A. ${10^{ - 5}}$
B. $12 \times {10^{ - 5}}$
C. $5 \times {10^{ - 5}}$
D. $7 \times {10^{ - 5}}$

Answer 1

Hint – For these types of questions, we must know the basic formulae of the magnetic chapter and how to apply in different situations of the coils i.e. if they are parallel or perpendicular.
Formula used – 1)${B_{net}} = \sqrt {B_1^2 + B_2^2}$
2) ${B_{net}} = \dfrac{{{\mu _0}}}{{4\pi }}(\dfrac{{2\pi }}{r})\sqrt {i_1^2 + i_2^2}$

Complete step-by-step solution -
__
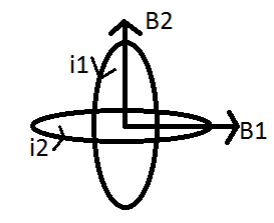
Given that,
${i_1}$=3A, ${i_2}$=4A and radius of coil = $2\pi$
We know that, ${B_{net}} = \sqrt {B_1^2 + B_2^2}$ (here we have used Pythagoras formula because both the fields are perpendicular to each other and their resultant will be calculated only like this)
And ${B_{net}} = \dfrac{{{\mu _0}}}{{4\pi }}(\dfrac{{2\pi }}{r})\sqrt {i_1^2 + i_2^2}$
${B_1}$ is the magnetic field in ring 1 and ${B_2}$ is magnetic field in ring 2.
${i_1}$is the current flowing in ring 1 and ${i_2}$ is current flowing in ring 2.
According to the flow of current, the magnetic fields will be perpendicular to the plane of the respective rings.
The value of $\dfrac{{{\mu _0}}}{{4\pi }}$ is ${10^{ - 7}}$.
On putting the value of radius and
Therefore, ${B_{net}} = {10^{ - 7}} \times (\dfrac{{2\pi }}{{2\pi }})\sqrt {{{(3)}^2} + {{(4)}^2}}$
${B_{net}} = 5 \times {10^{ - 7}}Wb/{m^2}$
Hence the correct answer to this question is $5 \times {10^{ - 7}}Wb/{m^2}$.
Hence the correct option is C.

Note – In solving this question we must know the application of formula according to the configuration of the two coils and the calculation mistake should be avoided. Since students generally make calculation mistakes in these questions. We advise the students to remember the formula of the magnetic field for rings at the axis and at the center. Remembering derivation will give you a brief knowledge to calculate the magnetic field for any other shape regarding a ring.