Question

Two communication cylindrical vessels contain mercury. The diameter of one vessel is n times larger than the diameter of the other, a column of water edge is poured into the vessel, the mercury level will rise in the right-hand vessel ([s= relative density of mercury and p = density of water) by
$A.\dfrac{{{n^h}}}{{{{\left( {n + 1} \right)}^2}s}} \\\ B.\dfrac{h}{{\left( {{n^2} + 1} \right)s}} \\\ C.\dfrac{h}{{{{\left( {n + 1} \right)}^2}s}} \\\ D.\dfrac{h}{{{n^2}s}} \\\$

Answer 1

In this question, we need to determine the rise in the height of the mercury level in the right-hand vessel such that the diameter of one vessel is ‘n’ times larger than the diameter of the other. For this, we will use Pascal’s law to equate the pressure at the two points at the same level into the vessels.

Complete step by step answer:
After adding water in the vessel, the mercury level in the right-hand side of the vessel increases by (say) x.

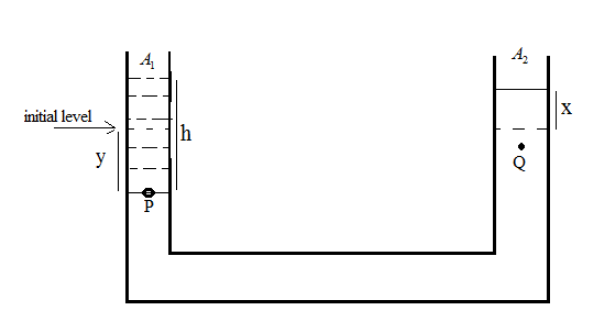
From the figure, we can say that
${A_1}$ is the area of left-hand side vessel
${A_2}$ is the area of right-hand side vessels
‘h’ is the height of the added water column
‘y’ is the decreasing level of mercury
‘x’ is the increasing level of mercury
Volume decrease in first vessel = volume increase in the second vessel so, we can write ${A_1}y = {A_2}x$
One vessel is larger than other; cording to the question the diameter of one vessel is n times larger than the diameter of the other so,
${d_2} = n{d_1} \\\ \Rightarrow{r_2} = n{r_1} \\\$
Substituting the values of the radius in the equation ${A_1}y = {A_2}x$, we get
${A_1}y = {A_2}x \\\ \Rightarrow\left( {\pi {r_1}^2} \right)y = \left( {\pi {r_2}^2} \right)x \\\ \Rightarrow\left( {\pi {r_1}^2} \right)y = \left( {\pi {{\left( {n{r_1}} \right)}^2}} \right)x \\\ \Rightarrow y = {n^2}x \\\$
Now, according to Pascal’s law in hydrostatic (no change in water levels) conditions, the pressure at the two points at the same level is the pressure at point P= pressure at point Q
${P_P} = {P^0} + h{\rho _w}g{\text{ and }}{P_Q} = {P^0} + (x + y){\rho _{Hg}}g$ where ${\rho _w}$ is the density of the water and ${\rho _{Hg}}$ is the density of the mercury.
So,

$${P_P} = {P_Q} \\\ \Rightarrow{P^0} + h{\rho _w}g = {P^0} + (x + y){\rho _{Hg}}g \\\ \Rightarrow h{\rho _w}g = (x + y){\rho _{Hg}}g \\\ \Rightarrow h{\rho _w} = (x + y){\rho _{Hg}} - - - - (i) \\\$$

But the density of mercury is yet to be found out, so we have a relative density of mercury:
$s = \dfrac{{density{\text{ }}of{\text{ Hg}}}}{{density{\text{ }}of{\text{ }}water}} \\\ \Rightarrow s = \dfrac{{{\rho _{Hg}}}}{{{\rho _w}}} \\\ \Rightarrow{\rho _{Hg}} = s{\rho _w} \\\$
Substituting this value in the equation (i), we get

$$h{\rho _w} = (x + y){\rho _{Hg}} \\\ \Rightarrow h{\rho _w} = (x + y)s{\rho _w} \\\ \Rightarrow h = (x + y)s \\\ \Rightarrow h = \left( {x + {n^2}x} \right)s \\\ \Rightarrow x\left( {{n^2} + 1} \right)s = h \\\ \therefore x = \dfrac{h}{{\left( {{n^2} + 1} \right)s}} \\\$$

Hence, the rise in the mercury level is given as $\dfrac{h}{{\left( {{n^2} + 1} \right)s}}$.
Hence,option B is correct.

Note: Do not forget to get the density of mercury using a relative density. Initially, the level of mercury in both the vessels will be at the same height, after adding water press will increase in one vessel (left-hand side) and the level of mercury will lower, while the level mercury in the other vessel will increase. According to Pascal’s law, the pressure will be constant at the two points at the same level in a hydrostatic system.