Question

Two coherent point sources ${S}_{1}$ and ${S}_{2}$ vibrating in phase emit light of wavelength $\lambda$. The separation between the sources is $2\lambda$. Consider a line passing through ${S}_{2}$ and perpendicular to the line ${S}_{1}{S}_{2}$. What is the smallest distance from ${S}_{2}$ where a minimum of intensity occurs?

Answer 1

Here, the smallest distance for minimum intensity is asked i.e. dark fringe. So, the path difference of light from point sources must be equal to the path difference for dark fringe. Substitute the values in above mentioned relation and solve it to obtain the relation for distance between ${S}_{2}$ and the point where fringes will be obtained. Now, assume the values of n=1,3,3 and so on and find the smallest distance.

Complete solution:

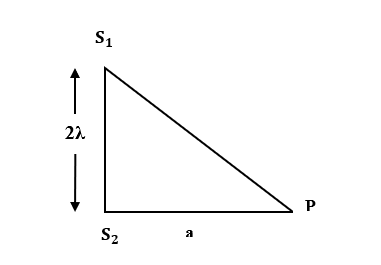
For minimum intensity of light, path difference of light from point sources must be equal to the path difference for dark fringe.
From the above figure, path difference is given by,
$path \quad difference= {S}_{1}P – {S}_{2}P$ …(1)
Path difference for dark fringe is given by,
$path \quad difference= \left(2n+1 \right) \dfrac {\lambda}{2}$ …(2)
From the equation. (1) and (2) we get,
${S}_{1}P – {S}_{2}P= \left(2n+1 \right) \dfrac {\lambda}{2}$ …(3)
From the above figure we can say,
${\left ({S}_{1}P\right )}^{2}= {\left({S}_{1}{S}_{2}\right)}^{2}+ {\left({S}_{2}P\right)}^{2}$
Substituting values in above equation we get,
${\left({S}_{1}P\right)}^{2}= {\left(2 \lambda\right)}^{2}+ {a}^{2}$
$\Rightarrow {\left({S}_{1}P\right)}^{2}= 4 {\lambda}^{2}+ {a}^{2}$
Taking the square root on both the sides we get,
${S}_{1}P= \sqrt{4{ \lambda}^{2}+ {a}^{2}}$
Now, substituting values in the equation. (3) we get,
$\sqrt{4{ \lambda}^{2}+ {a}^{2}}-a= \left(2n+1 \right) \dfrac {\lambda}{2}$
$\Rightarrow \sqrt{4{ \lambda}^{2}+ {a}^{2}}= \left(2n+1 \right) \dfrac {\lambda}{2}+a$
Squaring both the sides we get,
$4 {\lambda}^{2}+ {a}^{2}= { \left( 2n+1 \right) }^{ 2 }\dfrac { { \lambda }^{ 2 } }{ 4 } +a\lambda \left( 2n+1 \right) +{ a }^{ 2 }$
$\Rightarrow 4 {\lambda}^{2}= { \left( 2n+1 \right) }^{ 2 }\dfrac { { \lambda }^{ 2 } }{ 4 } +a\lambda \left( 2n+1 \right)$
Rearranging the above equation we get,
$a=\dfrac { 4{ \lambda }^{ 2 }-{ \left( 2n+1 \right) }^{ 2 }\dfrac { { \lambda }^{ 2 } }{ 4 } }{ \left( 2n+1 \right) \lambda }$
$\Rightarrow a=\dfrac { \dfrac { 16{ \lambda }^{ 2 }-{ \left( 2n+1 \right) }^{ 2 }{ \lambda }^{ 2 } }{ 4 } }{ \left( 2n+1 \right) \lambda }$
$\Rightarrow a=\dfrac { 16{ \lambda }^{ 2 }-{ \left( 2n+1 \right) }^{ 2 }{ \lambda }^{ 2 } }{ 4\left( 2n+1 \right) \lambda }$ …(4)
Case.1) If n=0 then, equation. (4) becomes,
$a=\dfrac { 15{ \lambda }^{ 2 } }{ 4\lambda }$
$\Rightarrow a=\dfrac { 15{ \lambda } }{ 4 }$
Case.2) If n=1 then, equation. (4) becomes,
$a=\dfrac { 7{ \lambda }^{ 2 } }{ 2\lambda }$
$\Rightarrow a=\dfrac { 7{ \lambda } }{ 2 }$
Case.3) If n=2 then, equation. (4) becomes,
$a=\dfrac { -9{ \lambda }^{ 2 } }{ 20\lambda }$
$\Rightarrow a=\dfrac { -9{ \lambda } }{ 20 }$
Thus, the smallest distance for minimum intensity is $\dfrac { 7{ \lambda } }{ 2 }$.

Note:
Here, we have not substituted n=3,4 and so on because the calculated values we obtained were negative. We know, distance can never be negative. Thus, we concluded the last positive value obtained for a as the smallest distance for minimum intensity. Also, students must remember what will be the path difference for maximum and minimum intensity. If the maximum intensity was asked then we would have considered the path difference for bright fringe as,
$path \quad difference= \left(2n-1 \right) \dfrac {\lambda}{2}$