Question

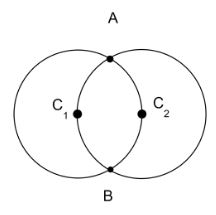
Two circular rings of identical radii and resistance of $36\Omega \;$ each are placed in such a way that they cross each other's centre ${C_1}$ ​ and ${C_2}$​ as shown in the figure. Conducting joints are made at intersection points A and B of the rings. An ideal cell of emf 20 volts is connected across AB. The power delivered by the cell is:

A. $80\,W$
B. $100\,W$
C. $120\,W$
D. $200\,W$

Answer 1

We can start by redrawing the figure. Then in order to find the power delivered by the cell, we have to find the equivalent resistance across the conducting joints, that is AB. The value of power delivered can be found using the formula that relates the power to voltage and resistance.

Formulas used:
The formula to find the power is given as,
$P = \dfrac{{{V^2}}}{R}$
Where $R$ is the equivalent resistance of the system and $V$ is the total voltage through the conducting points.
The equivalent can be found using the formula,
$\dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_4}}}$

Complete step by step answer:
We can start by redrawing the diagram with the necessary changes. In order to do that, we need the value of resistance across AB. To find the value of resistance, we have to split the figure with two circular rings into two parts before and after the conducting points. For this, we need to consider the value of resistance of two parts as shown in the figure

Now we have to find the resistance of the two parts individually.From the figure given in the question, we know that, $AC_1=AC_2=BC_1=BC_2=C_1C_2$. These values are equal to the radii of the circles.Then we can take the triangle $A_1C_1C_2$.Since all of the sides of this triangle are equal, all the angles are sixty degrees each and the line joining AB will divide the angle into two thirty degrees, this lets us consider the triangle $AC_1B$ and the angle $AC_1B$ is one hundred and twenty degrees as,
$A{C_1}B = 180 - \left( {30 + 30} \right) = 120$

The angle subtended in the centre of a circle is, $360^\circ$ and the resistance value of this angle is $36\Omega \;$
The value of resistance of one hundred and twenty degrees can be found using the formula,
${R_{120}} = \dfrac{{36}}{{360}} \times 120 = 12\Omega$
The same formula can be used to find the value of the rest of the circle or we can simply subtract and get, ${R_{240}} = 36 - 12 = 24\Omega$

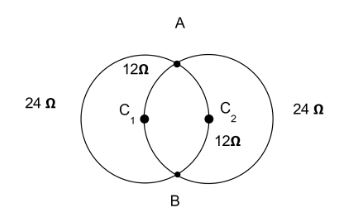
The four resistance values can be seen to be connected in parallel to one another. The equivalent can be found using the formula,
$\dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_4}}}$
Substituting the formulas, we get

\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{1}{{24}} + \dfrac{1}{{12}} + \dfrac{1}{{24}} + \dfrac{1}{{12}} \\\ \Rightarrow \dfrac{1}{{{R_P}}}= \dfrac{3}{{12}}$$ We can take the reciprocal of the value and get the equivalent resistance as, $$4\Omega $$. Now that we have the value of resistance, the power delivered can be found out using the formula, $$P = \dfrac{{{V^2}}}{R}$$ Substituting, we get $$P = \dfrac{{{V^2}}}{R} \\\ \Rightarrow P= \dfrac{{{{\left( {20} \right)}^2}}}{4} \\\ \therefore P= 100\,W$$ **Therefore, the correct answer is option (B).** **Note:** The power in an electric circuit element is a measure of how quickly it converts energy. In an electric circuit, some elements deliver power (that is, convert energy into the electrical form) and other elements absorb power (that is, convert energy from electrical energy into some other form). The formula to find the power we have used in the above question can be derived from the ohms law.We know that, $$I = \dfrac{V}{R}$$ and $$P = {I^2}R$$. Substituting the values we get the formula used in the question.