Question

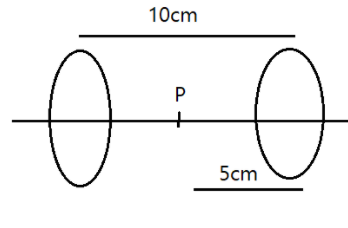
Two circular loops having the same radius $R=10cm$ and same current $\dfrac{7}{2}A$ are placed along the same axis as shown. If distance between their centre is $10\;cm$, find the net magnetic field at point $P$

& A.\dfrac{50{{\mu }_{0}}}{\sqrt{5}}T \\\ & B.\dfrac{28{{\mu }_{0}}}{\sqrt{5}}T \\\ & C.\dfrac{56{{\mu }_{0}}}{\sqrt{5}}T \\\ & D.\dfrac{56{{\mu }_{0}}}{\sqrt{3}}T \\\ \end{aligned}$$

Answer 1

We know that electricity and magnetism are interrelated. We know that a current carrying conductor can produce a magnetic field around itself. And similarly, a varying magnetic field induces a current in the wire which is kept in the near surrounding.

Formula: $B=\dfrac{\mu_{0}ir^{2}}{2(r^{2}+n^{2})^{\dfrac{3}{2}}}$

Complete answer:
We know that the magnetic field is an invisible force which is a vector that influences an electric charge and a few magnetic metals. Since it’s a vector clearly, it has both direction and magnitude. A magnet has two different poles, namely the North and the South Pole. Generally, the like poles attract, while the unlike poles repel. This is saying that, North Pole of one magnet repels from the north pole of another magnet, this is true for two South Pole also. However, if a North Pole of one magnet is brought near the south pole of another magnet, then they attract.
We also know that magnetic field $B$ at a axial point due to a circular current carrying loop is given as $B=\dfrac{\mu_{0}ir^{2}}{2(r^{2}+n^{2})^{\dfrac{3}{2}}}$, where $n$ is the radius of the loop and $r$ is the distance of the point from the centre of the loop.
Clearly, from the right hand thumb rule, since the magnetic field outside the loop is directed into the paper, we can say that the net magnetic field at P is the sum total of all the magnetic fields due to the current carrying loop.
Here, $n=5\times 10^{-2}m$,$r=10\times 10^{-2}m$ and $i=\dfrac{7}{2}A$
Then, substituting, we get, $B_{P}=2\times\dfrac{\mu_{0}\dfrac{7}{2}(0.1)^{2}}{2((0.1)^{2}+(0.5)^{2})^{\dfrac{3}{2}}}$
$\implies B_{P}=\dfrac{mu_{0}\dfrac{7}{2}(0.01)}{2((0.01)+(0.25))^{\dfrac{3}{2}}}$
$\therefore B_{P}=\dfrac{56\mu_{0}}{\sqrt 5}T$

Hence the correct answer is option $C.\dfrac{56{{\mu }_{0}}}{\sqrt{5}}T$ .

Note:
We know that the magnetic field is a vector quality, and hence has both direction and magnitude. We can also say that, the direction of the magnetic field is given from the right hand thumb rule, provided, the direction of the current is known.