Question

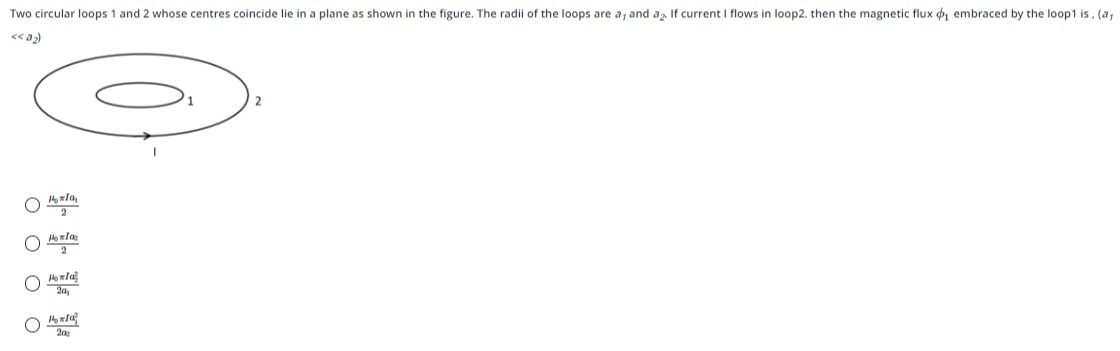
Two circular loops 1 and 2 whose centres coincide lie in a plane as shown in the figure. The radii of the loops are $a_1$ and $a_2$. If current I flows in loop2, then the magnetic flux $\phi_1$ embraced by the loop1 is, $(a_1 << a_2)$

• A. $\frac{\mu_0 \pi I a_1}{2}$
• B. $\frac{\mu_0 \pi I a_2}{2}$
• C. $\frac{\mu_0 \pi I a_1^2}{2a_1}$
• D. $\frac{\mu_0 \pi I a_1^2}{2a_2}$

Answer 1

Answer: (D)

$\frac{\mu_0 \pi I a_1^2}{2a_2}$

Answer 2

To find the magnetic flux $\phi_1$ embraced by loop 1 due to the current $I$ flowing in loop 2, we need to determine the magnetic field produced by loop 2 at the location of loop 1 and then multiply it by the area of loop 1.

Given:

• Radius of loop 1 = $a_1$
• Radius of loop 2 = $a_2$
• Current in loop 2 = $I$
• Condition: $a_1 << a_2$ (Loop 1 is much smaller than loop 2)
• Both loops are concentric and lie in the same plane.

1. Magnetic Field due to Loop 2:

   Since $a_1 << a_2$, the magnetic field produced by the larger loop (loop 2) can be considered approximately uniform over the entire area of the smaller loop (loop 1). The best approximation for this uniform field is the magnetic field at the center of loop 2.

   The magnetic field $B_2$ at the center of a circular loop of radius $a_2$ carrying current $I$ is given by:

   $B_2 = \frac{\mu_0 I}{2a_2}$

   This magnetic field is perpendicular to the plane of the loops.

2. Area of Loop 1:

   The area of loop 1, $A_1$, is given by:

   $A_1 = \pi a_1^2$

3. Magnetic Flux through Loop 1:

   The magnetic flux $\phi_1$ through loop 1 is the product of the magnetic field $B_2$ (assumed uniform over the area of loop 1) and the area $A_1$ of loop 1. Since the magnetic field is perpendicular to the plane of the loop, the angle between the magnetic field vector and the area vector is 0 degrees, so $\cos(0^\circ) = 1$.

   $\phi_1 = B_2 \times A_1$

   Substitute the expressions for $B_2$ and $A_1$:

   $\phi_1 = \left(\frac{\mu_0 I}{2a_2}\right) \times (\pi a_1^2)$

   $\phi_1 = \frac{\mu_0 \pi I a_1^2}{2a_2}$

The calculated magnetic flux matches the fourth option.