Question
Question: Two circular coils \( X \) and \( Y \) have equal number of turns and carry equal currents in the sa...
Two circular coils X and Y have equal number of turns and carry equal currents in the same sense and subtend the same solid angle at point (O) . If the smaller coil X is midway between O and Y , then if we represent magnetic induction due to bigger coil Y at O as BY , and that due to smaller coil X at O as BX , then
A. BXBY=1
B. BXBY=2
C. BXBY=21
D. BXBY=41
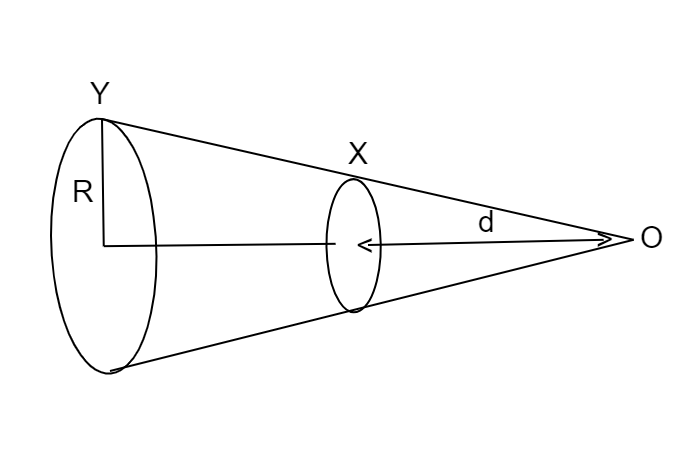
Solution
In this question, we are given two coils carrying the same current and having the same number of turns. As they subtend the same solid angle at point O and the smaller coil is midway between the larger coil and point O . By using geometry we can say, Radius of the larger coil is twice the radius of smaller coil and we can find out the magnetic field due to coil at a distance x using the formula B=2(R2+x2)3/2μ0NIR2
Magnetic field due at the axis of a circular current-carrying coil, B=2(R2+x2)3/2μ0NIR2
Where B is the magnetic field at the axis
R is the radius of the coil
I is the current carried by the coil
N is the number of turns in the coil
x is the distance from the center of the coil.
Complete step by step answer:
We are given two coils X and Y having an equal number of turns N and carrying an equal amount of current I
Distance of centre of coil X from the point O is d
As coil X is midway between Y and O ,
Distance of centre of coil Y and O is 2d
Let radius of coil Y be R and radius of coil X be r
Both the coils subtend same angle at point O thus,
dr=2dR
⇒R=2r
Now, the magnetic field at point O due to bigger coil Y , BY=2(R2+(2d)2)3/2μ0NIR2
Substituting R=2r we get,
⇒BY=2(4r2+4d2)3/2μ0NI(4r2)
⇒BY=2×8(r2+d2)3/2μ0NI(4r2)
⇒BY=4(r2+d2)3/2μ0NIr2
Magnetic field at point O due to smaller coil X , BX=2(r2+d2)3/2μ0NIr2
Therefore, BXBY=2(r2+d2)3/2μ0NIr24(r2+d2)3/2μ0NIr2⇒21
BXBY=21
Hence, the correct option is option C.
Note:
Magnetic field at the center of the coil is maximum and is equal to BX=2Rμ0NI . The magnetic field along the axis of the coil keeps on decreasing as we move away from the center of the coil and at far points, x≫R magnetic field becomes, B=2x3μ0NIR2 .
