Question

Two circles with centres $O,{{O}^{'}}$ of radius 3cm and 4cm, respectively intersect at two points P and Q, such that $OP,{{O}^{'}}P$ are tangents to the two circles. Find the length of the common chord PQ.
a) 4.8
b) 5.4
c) 3.2
d) 7.9

Answer 1

Hint:Draw the figure and consider the triangles formed $OP{{O}^{'}},OQ{{O}^{'}}$. Thus prove $\angle PO{{O}^{'}}=\angle QO{{O}^{'}}$. Now consider R the point where $O{{O}^{'}},PQ$ intersect. Prove that PR = RQ. Thus by Pythagoras theorem, find the length $O{{O}^{'}}$. Prove $OP\bot O{{P}^{'}}$. Thus find the length of PQ from the figure we can understand that 2 circles are given. The centre of the first circle is O and of the other circle is ${{O}^{'}}$. Now these two circles meet at the point P and Q.

Complete step-by-step answer:

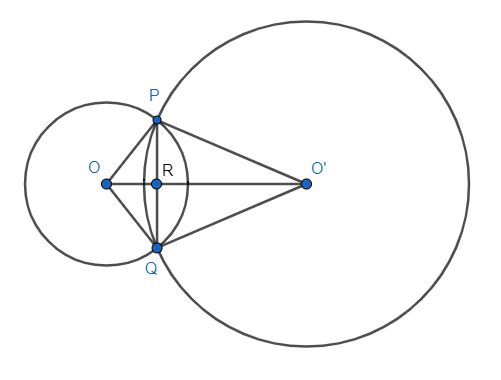
Now let us assume that $O{{O}^{'}}$ intersect PQ at point R, as shown in the figure. These two triangles are formed. Now let us consider $\Delta OP{{O}^{'}},\Delta OQ{{O}^{'}}$ from the figure
OP = OQ [they are radius of the 1st circle and they are equal]
$\begin{aligned} & O{{O}^{'}}=O{{O}^{'}}\left[ \text{this side is common to both the triangle} \right] \\\ & O{{P}^{'}}=O{{Q}^{'}}\left[ \text{they are radius of the 2nd circle and they are equal} \right] \\\ \end{aligned}$
Thus we can say that both triangles are equal by SSS congruence i.e. all sides of $\Delta OP{{O}^{'}}$ is equal to all the three sides of $\Delta OQ{{O}^{'}}$. Thus by SSS congruence,
$\Delta OP{{O}^{'}}=\Delta OQ{{O}^{'}}$
As the triangles are equal, their angle will also be equal. So we can say that
$\angle PO{{O}^{'}}=\angle QO{{O}^{'}}$
Now, let us consider triangle POR and QOR.
OP = OQ, they are radius of the same circle
OR = OR, common side to both triangles.
We have to prove,
$\angle POR=\angle QOR$
Thus by SAS congruence, two sides and one angle of one triangle is equal to two sides and one angle of another triangle. Thus by SAS congruence we can say that
$\Delta POR=\Delta QOR$
Thus CPCT (corresponding points of congruent triangle) we say that
$\angle ORP=\angle ORQ$
From the figure, you can say that
$\angle ORP+\angle OPQ={{180}^{\circ }}$
i.e. they are a linear pair, thus we got that
$\begin{aligned} & \angle OPR=\angle ORQ \\\ & \angle ORP+\angle ORP={{180}^{\circ }} \\\ & 2\angle ORP={{180}^{\circ }} \\\ & \angle ORP={{90}^{\circ }} \\\ & \therefore \angle ORP=\angle ORQ={{90}^{\circ }} \\\ \end{aligned}$
Hence, we can say that PR is equal to RQ, i.e. PR = RQ. Perpendicular from the centre bisect the chord. Thus we can say that OP is perpendicular to $O{{P}^{'}}$.
In $\Delta OP{{O}^{'}}$, by taking the Pythagoras theorem
${{\left( O{{O}^{'}} \right)}^{2}}={{\left( OP \right)}^{2}}+{{\left( {{O}^{'}}P \right)}^{2}}$
From the equation its been told that the radius of 1st circle is 3cm i.e. OP = OQ = 3cm. Similarly in the second circle, the radius is 4cm. i.e.
$\begin{aligned} & {{O}^{'}}={{O}^{'}}Q=4cm \\\ & {{\left( O{{O}^{'}} \right)}^{2}}={{\left( OP \right)}^{2}}+{{\left( {{O}^{'}}P \right)}^{3}} \\\ & ={{3}^{2}}+{{4}^{2}}=9+16=25 \\\ & O{{O}^{'}}=\sqrt{25}=5cm \\\ \end{aligned}$
We have found the length of $O{{O}^{'}}$ as 5cm. Let us consider the length of OR as x.
$\begin{aligned} & OR=x \\\ & O{{O}^{'}}=OR+R{{O}^{'}} \\\ & \therefore R{{O}^{'}}=O{{O}^{'}}-OR \\\ & =5-x \\\ \end{aligned}$
Thus consider the length of $OR=x,R{{O}^{'}}=5-x$ . Now from $\Delta {{O}^{'}}PR$, by Pythagoras theorem we can write as,
$\begin{aligned} & {{\left( {{O}^{'}}P \right)}^{2}}={{\left( {{O}^{'}}R \right)}^{2}}+{{\left( PR \right)}^{2}} \\\ & \therefore {{\left( PR \right)}^{2}}={{\left( {{O}^{'}}P \right)}^{2}}-{{\left( {{O}^{'}}R \right)}^{2}} \\\ & ={{4}^{2}}-{{\left( 5-x \right)}^{2}} \\\ & =16-\left( 25+{{x}^{2}}-10x \right) \\\ & \because {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab \\\ & {{\left( PR \right)}^{2}}=16-25-{{x}^{2}}+10x........................\left( i \right) \\\ \end{aligned}$
From triangle OPR, by Pythagoras theorem

& {{\left( {{O}^{'}}P \right)}^{2}}={{\left( {{O}^{'}}R \right)}^{2}}+{{\left( PR \right)}^{2}} \\\ & {{\left( PR \right)}^{2}}={{\left( OP \right)}^{2}}-{{\left( OR \right)}^{2}}={{3}^{2}}-{{x}^{2}}=9-{{x}^{2}}.......................\left( ii \right) \\\ \end{aligned}$$ Now let us equate (i) and (ii) $\begin{aligned} & 9-{{x}^{2}}=16-25-{{x}^{2}}+10x \\\ & 9+25-16=10x \\\ & 10x=18 \\\ & \therefore \dfrac{18}{10}=\dfrac{9}{5} \\\ \end{aligned}$ Thus we got the value of $x=\dfrac{9}{5}$ . Now, put the value of x in equation (ii) $\begin{aligned} & {{\left( PR \right)}^{2}}=9-{{x}^{2}}={{\left( \dfrac{9}{5} \right)}^{2}}=\dfrac{9\times 25-81}{25}=\dfrac{225-81}{25}=\dfrac{144}{25} \\\ & \therefore {{\left( PR \right)}^{2}}=\dfrac{144}{25} \\\ & PR=\sqrt{\dfrac{144}{25}}=\dfrac{12}{5} \\\ & \therefore PR=RQ=\dfrac{12}{5} \\\ \end{aligned}$ We found that PR = RQ. Thus PQ = PR + RQ (from figure) $=\dfrac{12}{5}+\dfrac{12}{5}=\dfrac{24}{5}=4.8cm$ Thus we got the length of PQ as 4.8cm, the length of the common chord of the circle, PQ = 4.8cm. So, option (a) is correct Note: It is important that you prove the congruence of the triangle we obtained from the figure. So that we can prove R is the midpoint of PQ. i.e. PR = RQ. Don’t immediately substitute the radius to get the value, which you may think is the right way.