Solveeit Logo
Login

Question

Question: Two circles touch each other externally at P. AB is a common tangent to the circles touching them at...

Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value ∠APB\angle APB is
A. 30∘{30^ \circ }
B. 45∘{45^ \circ }
C. 60∘{60^ \circ }
D. 90∘{90^ \circ }

Explanation

Solution

First we will find the angles of the triangles having radii as the sides of the triangle using properties like angles opposite to equal sides. Now we will find the measures of the angles of the triangle of which ∠APB\angle APB is an angle, resulting in an equation.
Now using the property of a straight line that sum of all angles on a straight line measures 180∘{180^ \circ }we’ll get another equation.
Solving the equation formed we’ll get the measure of ∠APB\angle APB.

Complete step-by-step answer:
Given data: Both circles touch each other at P
AB is the common tangent touching the circles at A and B
Let the centers of the circle be L and M

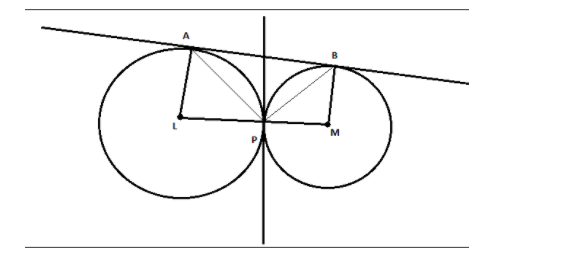
Let ∠LPA=α\angle LPA = \alpha and ∠MPB=β\angle MPB = \beta
In triangle ALP, we know that AL=LPAL = LP as both are the radius of the circle, therefore angles opposite to equal sides state that angle opposite sides will also be equal i.e. ∠LPA=∠LAP\angle LPA = \angle LAP
∴∠LAP=α\therefore \angle LAP = \alpha
Similarly, in triangle BMP, BM=PMBM = PM as they are the radius of the circle
Therefore, ∠MPB=∠MBP\angle MPB = \angle MBP
∴∠MBP=β\therefore \angle MBP = \beta
We know that the tangent to a circle is always perpendicular to the radius at the point tangency.
Therefore, LA⊥AB LA \bot AB\, and BM⊥AB BM \bot AB\,
i.e. ∠LAP+∠PAB=90∘\angle LAP + \angle PAB = {90^ \circ }
Now substituting ∠LAP=α\angle LAP = \alpha , we get,
⇒∠PAB=90∘−α\Rightarrow \angle PAB = {90^ \circ } - \alpha
Similarly, ∠MBP+∠PBA=90∘\angle MBP + \angle PBA = {90^ \circ }
Now substituting ∠MBP=β\angle MBP = \beta
⇒∠PBA=90∘−β\Rightarrow \angle PBA = {90^ \circ } - \beta
We know that the sum of angles of triangle measures 180∘{180^ \circ }
Therefore, in triangle APB
⇒∠PAB+∠PBA+∠APB=180∘\Rightarrow \angle PAB + \angle PBA + \angle APB = {180^ \circ }
Substituting ∠PBA=90∘−β\angle PBA = {90^ \circ } - \beta and ∠PAB=90∘−α\angle PAB = {90^ \circ } - \alpha
⇒180∘−α−β+∠APB=180∘\Rightarrow {180^ \circ } - \alpha - \beta + \angle APB = {180^ \circ }
⇒α+β=∠APB\Rightarrow \alpha + \beta = \angle APB
Now we know that sum of all angles on a straight line measures 180∘{180^ \circ }
Therefore, ∠LPA+∠APB+∠MPB=180∘\angle LPA + \angle APB + \angle MPB = {180^ \circ }
Now substituting the values of ∠LPA,∠MPB\angle LPA,\angle MPB , we get,
⇒α+β+∠APB=180∘\Rightarrow \alpha + \beta + \angle APB = {180^ \circ }
Now substituting α+β=∠APB\alpha + \beta = \angle APB, we get,
⇒2∠APB=180∘\Rightarrow 2\angle APB = {180^ \circ }
Dividing by 2, we get,
⇒∠APB=90∘\Rightarrow \angle APB = {90^ \circ }
Hence, Option (D) is correct.

Note: Here we have given the tangent of the circle, so let us discuss some properties related to the tangent of a circle
A tangent of a circle always touches the circle at a single point.
Tangent is always perpendicular to the radius made at the point of tangency.
The length of two tangents drawn to a single point to a circle is always equal.