Question

Two circles of radii $5cm$ and $3cm$ intersect at two points and the distance between their centers is $4cm$. Find the length of the common chord.

Answer 1

A circle is the path of a point which moves in a plane so that it remains at a constant distance from a fixed point in the plane. The fixed point is called the center and the constant distance from a fixed point in the plane. A line segment joining any two points of a circle is called a chord of the circle. The perpendicular from the center of a circle to a chord bisects the chord. Pythagoras theorem, “in a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides”.

Complete step-by-step answer:
Let us draw two circles of radii $5cm$ and $3cm$ intersect at two points A and B on the circumference of the circle.

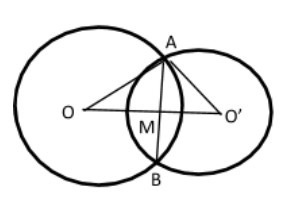
Let O and O’ be the centers of the circles of radii $5cm$ and $3cm$ respectively.
Let AB be the common chord of the two circles.
As the line of centers is the perpendicular bisector of the common chord,
OO’$\bot$AB and M is midpoint of AB.
Let AM $= x$ cm and OM $= y$ cm.
As OO’ $= 4$ cm (given), so MO’$= (4 - x)cm$.
In $\Delta OMA$,$\angle M = 90^\circ$, by Pythagoras theorem,
$O{A^2} = O{M^2} + A{M^2}$
Substituting the values of OA, OM and AM in the above equation, we get
$\Rightarrow {5^2} = {y^2} + {x^2}$ ………....(i)
Now, In$\Delta O'MA$,$\angle M = 90^\circ$, by Pythagoras theorem,
$O'{A^2} = OM{'^2} + A{M^2}$
Substituting the values of O’A, OM’ and AM in the above equation, we get
$\Rightarrow {3^2} = {(4 - y)^2} + {x^2}$ ………….(ii)
Subtracting equation (ii) from (i), we get
$25 - 9 = {y^2} - {(4 - y)^2}$
By applying identity ${(a - b)^2} = {a^2} + {b^2} - 2ab$, we get
$16 = {y^2} - ({4^2} + {y^2} - 2 \times 4 \times y)$
Simplifying the bracket first, we get
$\Rightarrow 16 = {y^2} - (16 + {y^2} - 8y)$
As we know, $( - ) \times ( + ) = ( - )$and$( - ) \times ( - ) = ( + )$, therefore
$16 = {y^2} - 16 - {y^2} + 8y$
Cancelling ${y^2}$from the R.H.S as one is having a positive sign and another is having a negative sign, we get
$16 = 8y - 16$
Transposing 16 from R.H.S to L.H.S, we get
$\Rightarrow 16 + 16 = 8y$
$\Rightarrow 32 = 8y$
Now as 8 is multiplied by y in the R.H.S, so it will shift into the denominator of the L.H.S.
$\Rightarrow \dfrac{{32}}{8} = y$
As we know $8 \times 4 = 32$, therefore
$4 = y$
Now putting $4 = y$ in (ii), we get
${3^2} = {(4 - 4)^2} + {x^2}$
$\Rightarrow {3^2} = {0^2} + {x^2}$
$\Rightarrow {3^2} = {x^2}$
Taking square root of boot sides, we get
$3 = x$
$\therefore$Length of common chord $AB = 2 \times AM$
$\Rightarrow AB = 2 \times x$
As $x = 3cm$, therefore $AB = (2 \times 3)cm$
$\Rightarrow AB = 6cm$
$\therefore$Length of common chord$AB = 6cm$.

Note: In the above question, we observe that $x = 4 \Rightarrow$MO’=0
$\Rightarrow$The points M and O’ coincide.
$\Rightarrow$The center of the smaller circle lies on the common chord.
$\Rightarrow$The common chord is a diameter of the smaller circle.