Question
Question: Two children are playing a game in which they try to hit a small box on the floor with a marvel fire...
Two children are playing a game in which they try to hit a small box on the floor with a marvel fired from a spring-loaded gun that is mounted on a table. The target box is at a horizontal distance D = 2.2m from the edge of the table. Bobby compresses the spring 1.7cm, but the center of the marble falls 27cm short of the center of the box. How far should Rhoda compress the spring to score a direct hit? Assume that neither the spring nor the ball encounters friction in the gun.
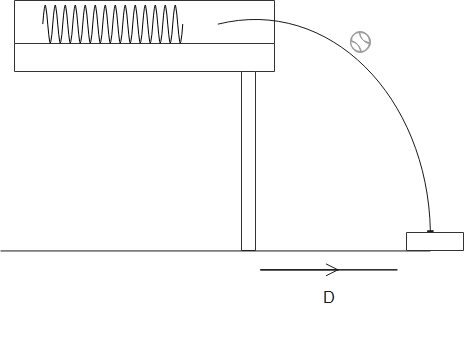
Solution
For solving this question, we would require the concept of Range from projectile motion and the concept of spring forces and the conservation of mechanical energy. We see from the diagram that the value of desired range D is given and the value of range Bobby got is given.
Complete step by step solution:
Note that the question is of a projectile in horizontal direction launched from its maximum height, thus the vertical component of the launch is zero. The range of the ball can be found by the product of time taken and the initial speed of the ball. Now this speed is generated as the compression potential energy of the spring is converted to the kinetic energy of the ball. Now for horizontal projectiles, the height can also be easily found out. Thus the formulas are:
Distance $$$$$x = {v_0}t - - - - (1),where{v_0}istheinitialspeedofthelaunch.Nowtheheightofthetableis:h = \dfrac{1}{2}g{t^2} - - - - (2).Nowtisthetimerequiredforthetravelfromtabletodesiredpoint.Bysolving1and2wegetx = {v_0}\sqrt {2h/g} - - - - (3).Thuswecanseethatdistanceoftravelisdirectlyproportionaltotheinitialvelocityoftheball.Thus{x^{}} \propto {v_0}^{} - - - - (4)NowforBobby’sshot,weseex = 2.2 - 0.27 = 1.93m.Nowforthespringwesee,ifit′scompressedtoalengthl,thespringpotentialenergyis\dfrac{1}{2}k{l^2}.Nowbyconservationofmechanicalenergy,weseethispotentialisconvertedtokineticoftheball,hence\dfrac{1}{2}k{l^2} = \dfrac{1}{2}m{v_0}^2.Asbothspringconstantandmassareconstantthuswecansaythelengthofcompressedspringisproportionaltotheinitialvelocity.Thus{l^{}} \propto {v_0}^{} - - - - (5)$
From 5 and 4 we can say: l1l2=x1x2
⇒l2=(1.932.2)×1.1=1.25cm
Note: These questions require the concept of energy transformation to solve, note that you do not make mistakes while making the relations as direct proportions or indirect proportions. The formulas of range, maximum height are to be remembered from projectile motion.
