Question

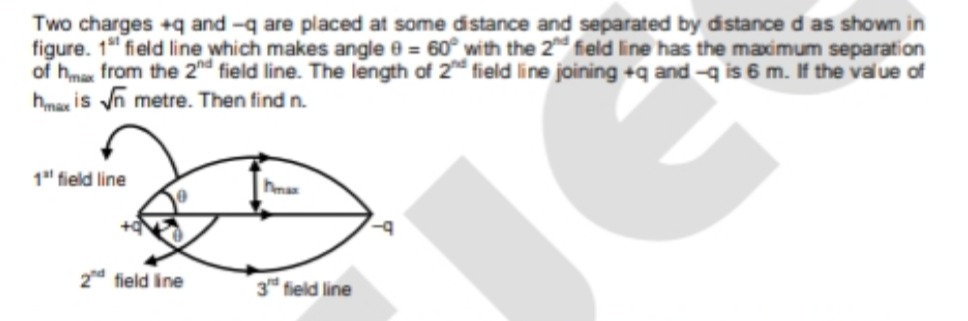
Two charges +q and -q are placed at some distance and separated by distance d as shown in figure. 1st field line which makes angle $\theta$ = 60° with the 2nd field line has the maximum separation of $h_{max}$ from the 2nd field line. The length of 2nd field line joining +q and -q is 6 m. If the value of $h_{max}$ is $\sqrt{n}$ metre. Then find n.

Answer 1

n = 3

Answer 2

1. Choose a coordinate system with +q at (0,0) and –q at (6,0). The 2nd field line is the straight line joining these charges (the horizontal line).

2. The 1st field line starts from (0,0) making a 60° angle with the horizontal. Assume it is a circular arc joining (0,0) to (6,0). Its circle must be tangent at (0,0) to the direction (cos 60, sin 60) = (0.5, √3⁄2).

3. For a circle with center (3, k) (since it must lie on the perpendicular bisector of the chord joining (0,0) and (6,0)), the tangency condition at (0,0) requires that the radius vector (from the center to (0,0)) is perpendicular to the tangent (0.5, √3⁄2). Writing the radius from (3, k) to (0,0) as (–3, –k), the dot product with (0.5, √3⁄2) must vanish:

   $$-3\,(0.5) + (-k)\,\left(\frac{\sqrt3}{2}\right)= 0 \quad\Longrightarrow\quad -1.5 - \frac{\sqrt3}{2}\,k = 0.$$

   Solving gives:

   $$k = -\frac{1.5 \times 2}{\sqrt3} = -\frac{3}{\sqrt3} = -\sqrt3.$$

   Thus, the circle’s center is (3, –√3) and its radius is

   $$R = \sqrt{(3-0)^2 + (-\sqrt3-0)^2} = \sqrt{9+3} = 2\sqrt3.$$

4. The maximum separation $h_{\text{max}}$ between the 1st (curved) and the 2nd (straight horizontal) field lines is the vertical distance of the arc from the chord. For a circular arc with chord endpoints at (0,0) and (6,0), this maximum distance occurs at the midpoint (3,0). From the circle, at $x=3$,

   $$(3-3)^2+(y+ \sqrt3)^2 = (2\sqrt3)^2=12 \quad\Longrightarrow\quad (y+\sqrt3)^2 =12.$$

   Taking the positive square root (since the 1st field line curves upward),

   $$y+\sqrt3 = 2\sqrt3 \quad\Longrightarrow\quad y = \sqrt3.$$

   Hence, $h_{\text{max}} = \sqrt3$ metres.

5. We are told $h_{\text{max}} = \sqrt{n}$ m, so equating, $\sqrt{n} = \sqrt{3}$ which gives $n = 3$.

Core Explanation:

• Use circle geometry with chord 6 m and tangent condition (angle 60°) at the positive charge to determine the circle.
• Compute the maximum (vertical) deviation of the circular arc from the chord at its midpoint; it turns out to be $\sqrt3$ m.
• Equate $\sqrt{n} = \sqrt3$ to find $n = 3$.