Question
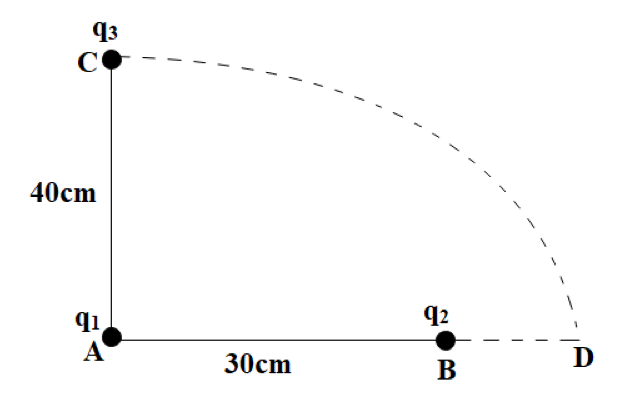
Question: Two charges \({{q}_{1}}\) and \({{q}_{2}}\) are placed 30cm apart, as shown in figure. A third charg...
Two charges q1 and q2 are placed 30cm apart, as shown in figure. A third charge q3 is moved along the arc of a circle of radius 40cm from C to D. the change in the potential energy of the system is 4πε0q3k , where k is
A.8q1
B.6q1
C.8q2
D.6q2
Solution
We are given two charges and a third charge is entering their in space. These already present charges had some potential energy due to each other and third charge at point C. This will be considered as the initial potential energy of the system. When a third charge is introduced, they develop more potential energy due to it. This sums up as the final potential energy. We will subtract the initial and final potential energies to get the change in potential energy.
Complete answer:
The potential energy, U of any charged body is given as:
U=4πε01.rq1q2
Where,
q1= charge on first body
q2= charge on second body
r= distance between the two charges
We have AB=30cm,AC=40cm, thus by Pythagorean triplets, BC is given as:
BC=AB2+AC2⇒BC=302+402⇒BC=900+1600⇒BC=2500
∴BC=50cm
Also,
BD=AD−AB⇒BD=40−30⇒BD=10cm
For a discrete system of charges, the potential energy is expressed as the sum of all potential energies of the system.
U=4πε01[r12q1q2+r23q2q3+r13q1q3]
For the initial potential energy when q3 is at point C,
r12=AB=30cm=0.3m, r23=BC=50cm=0.5m, r13=AC=40cm=0.4m
The potential energy is calculated as:
Ui=4πε01[ABq1q2+BCq2q3+ACq1q3]
⇒Ui=4πε01[0.3q1q2+0.5q2q3+0.4q1q3] ………………… equation (1)
For the final potential energy when q3 is at point D,
r12=AB=30cm=0.3m, r23=BD=10cm=0.1m, r13=AD=40cm=0.4m
The potential energy is calculated as:
Uf=4πε01[ABq1q2+BDq2q3+ADq1q3]
⇒Uf=4πε01[0.3q1q2+0.1q2q3+0.4q1q3] ………………… equation (2)
Change in potential energy= final potential energy – initial potential energy
⇒ΔU=Uf−Ui
From equation (1) and (2),
⇒ΔU=4πε01[0.3q1q2+0.1q2q3+0.4q1q3]−4πε01[0.3q1q2+0.5q2q3+0.4q1q3]
Taking 4πε01 common, we get
⇒ΔU=4πε01[0.3q1q2+0.1q2q3+0.4q1q3−0.3q1q2−0.5q2q3−0.4q1q3]
⇒ΔU=4πε01[q2q3(0.11−0.51)]⇒ΔU=4πε01[q2q3(0.1(0.5)0.5−0.1)]
⇒ΔU=4πε01[q2q30.050.40]
⇒ΔU=4πε018q2q3
Therefore, the change in potential energy is equal to 4πε018q2q3.
Hence, the correct option is (C) 8q2
Note:
Every charged body has its own electric potential. However, the potential energy of any charged body is always measured with respect to some other charged body in its vicinity. This is because any charged body develops a potential energy due to interaction with another charged body near it. The potential energy of any charged body is zero if it is isolated in space.
