Question

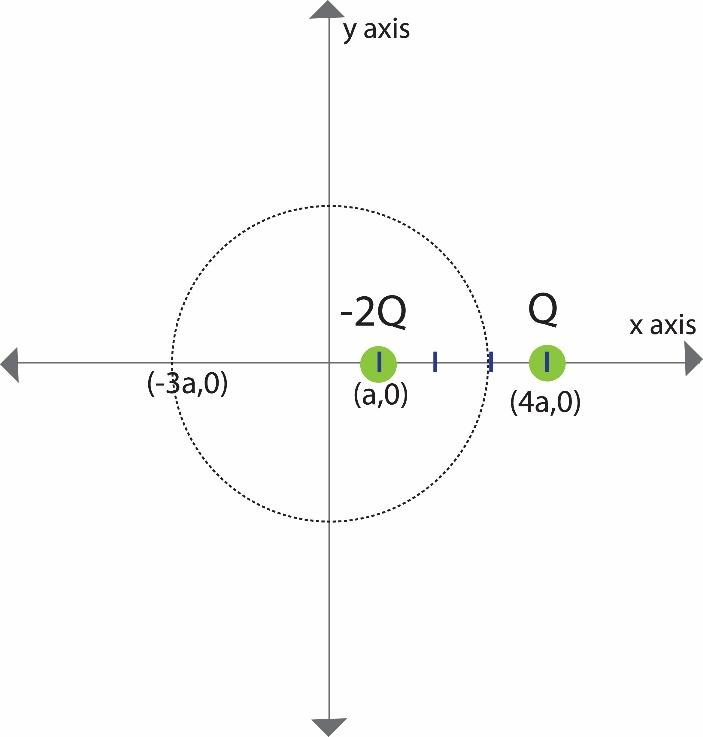
Two charges of magnitudes -2Q and Q are located at points (a,0) and (4a,0) respectively. What is the electric flux due to these charges through a sphere of radius 3a with its centre at origin?

Answer 1

From the given positions of the charges, draw the diagram of how the system looks in the space. Apply Gauss’s law on the sphere to find the flux. Gauss’s law states the dependency of a charge inside a closed surface to the flux through it.

Formula used: Formula of flux from Gauss’s law for a charge Q enclosed within a closed surface.
$\Phi =\dfrac{Q}{{{\varepsilon }_{o}}}$

Complete answer:
Electric field is a property associated with a point in space which a charge experiences. The magnitude and direction of the electric field determine the tendency of the charge to move is called electric field strength or electric field intensity or simply the electric field. Electric field lines are usually considered to start on positive electric charges and to end on negative charges.

Electric flux is a property of an electric field which gives us the number of field lines that pass-through a given area. Field lines directed inside a closed surface are considered negative while those directed outside of a closed surface are considered positive.
The formula for flux through a surface S, where the electric field is given as E is given as
$\Phi =\oint\limits_{S}{E.dA}$
As directed in the question, the diagram of the space is represented in the figure.
Gauss’s law states that the flux through a closed surface depends only on the charge Q enclosed by it. The formula is given by
$\Phi =\dfrac{Q}{{{\varepsilon }_{o}}}$
Therefore, only -2Q charge affects the flux from the figure, asked in the question and the value for the flux is given by
$\Phi =-\dfrac{2Q}{{{\varepsilon }_{o}}}$

Note: Do not include the +Q charge in the calculation. Gauss's law states that a charge outside will have no effect. To understand this, consider a closed surface and imagine a charge just outside it. All the field lines that enter the sphere escape it as well making the net field lines passing through the sphere zero.