Solveeit Logo
Login

Question

Question: Two charges of \( + 25 \times {10^{ - 9}}\) coulombs and \( - 25 \times {10^{ - 9}}\) coulomb are pl...

Two charges of +25×10−9 + 25 \times {10^{ - 9}} coulombs and −25×10−9 - 25 \times {10^{ - 9}} coulomb are placed 6m apart. Find the electric field intensity ratio at points 4m from the centre of the electric dipole.
(i) On axial line
(ii) On equatorial line
(A) 100049\dfrac{{1000}}{{49}}
(B) 491000\dfrac{{49}}{{1000}}
(C) 50049\dfrac{{500}}{{49}}
(D) 49500\dfrac{{49}}{{500}}

Explanation

Solution

To find the electric field intensity an axial line or equatorial line due to +q and –q charge we use the point charge formula i.e., E=kqr2E = \dfrac{{kq}}{{{r^2}}} and after then acceleration to the direction of electric field we can find the complete solution for axial & equatorial.

Complete step by step solution:
We have to calculate the electric field intensity on the axial line and on the equatorial line.
Case-I
For axial line

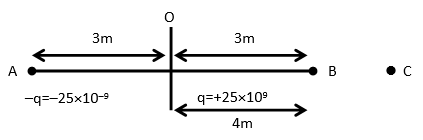
The electric field intensity due to point charge −q=−kqr2 - q = \dfrac{{ - kq}}{{{r^2}}}
For –q charge r is the distance between A & C i.e., =4+3=7m = 4 + 3 = 7m
Eq=−9×109×25×10−97×7=−25×949{E_q} = \dfrac{{ - 9 \times {{10}^9} \times 25 \times {{10}^{ - 9}}}}{{7 \times 7}} = \dfrac{{ - 25 \times 9}}{{49}}
Now, the electric field intensity due to point charge +q is =kqr2 = \dfrac{{kq}}{{{r^2}}}
Here r is distance between B & C i.e., 4−3=1m4 - 3 = 1m
E+q=9×109×25×10−91×1=25×9{E_{ + q}} = \dfrac{{9 \times {{10}^9} \times 25 \times {{10}^{ - 9}}}}{{1 \times 1}} = 25 \times 9
Hence the electric field intensity at point C i.e., on axial line is Ea=E+q+E−q{E_a} = {E_{ + q}} + {E_{ - q}}
=25×9−25×949=25×9(1−149)= 25 \times 9 - \dfrac{{25 \times 9}}{{49}} = 25 \times 9\left( {1 - \dfrac{1}{{49}}} \right)
Ea=(4849)(25×9){E_a} = \left( {\dfrac{{48}}{{49}}} \right)(25 \times 9)
Ea=10,80049{E_a} = \dfrac{{10,800}}{{49}} ……(i)

Case-II
If point C is situated on equatorial line then electric field intensity can be calculated as

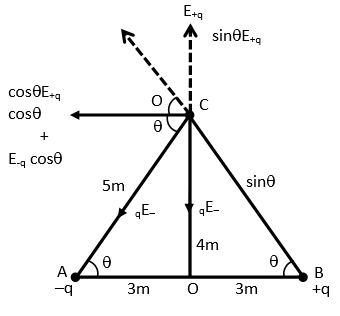
Here magnitude of electric field intensity for +q & -q are same i.e., E=kqr2E = \dfrac{{kq}}{{{r^2}}}
Here r is distance between +q and –q to point C i.e., AC & BC which are equal
So, AC=BC=r=(3)2+(4)2AC = BC = r = \sqrt {{{(3)}^2} + {{(4)}^2}}
r=5mr = 5m
Then, E+q=E−q=E=9×109×25×10−95×5{E_{ + q}} = {E_{ - q}} = E = \dfrac{{9 \times {{10}^9} \times 25 \times {{10}^{ - 9}}}}{{5 \times 5}}
E=25×925=9NCE = \dfrac{{25 \times 9}}{{25}} = 9\dfrac{N}{C}
Now, the total electric field intensity at point C i.e., on equatorial line according to diagram is given as –
Eeq=E+qcos⁡θ+E−qcos⁡θ{E_{eq}} = {E_{ + q}}\cos \theta + {E_{ - q}}\cos \theta
=2Ecos⁡θ= 2E\cos \theta
From diagram cos⁡θ=35\cos \theta = \dfrac{3}{5}
Eeq=2×9×35=545{E_{eq}} = 2 \times 9 \times \dfrac{3}{5} = \dfrac{{54}}{5} …..(2)
From equation (1) & (2) we can easily calculate the ratio of Ea{E_a} & Eeq{E_{eq}}
So, (1)(2)\dfrac{{(1)}}{{(2)}}
EaEeq=10,80049×554\dfrac{{{E_a}}}{{{E_{eq}}}} = \dfrac{{10,800}}{{49}} \times \dfrac{5}{{54}}
54,00049×54\dfrac{{54,000}}{{49 \times 54}}
So, ratio of Ea{E_a} & Eeq{E_{eq}}
Ea:Eeq=1000:49{E_a}:{E_{eq}} = 1000:49

So, the correct answer is (A) 100049\dfrac{{1000}}{{49}}

Note: In this type of question basically we use electric field intensity due to point charge separately and then add them. But in many cases of dipole numericals a<<<ra < < < r i.e., distance from the centre of dipole is very large comparatively the distance between the 2 charges. So, in this case we can directly use 2 formulas which are given as
Ea=2kpr3{E_a} = \dfrac{{2kp}}{{{r^3}}}
Eeq=krr3{E_{eq}} = \dfrac{{kr}}{{{r^3}}}
Where p is dipole moment of electric dipole i.e., p=qap = qa