Question

Two charges $5\mu C$and $-3\mu C$are located 16 cm apart. At what point on the line joining the two charges is the electric potential zero?

Answer 1

There are two cases to consider. In the first case, the point at which the potential is zero is considered to be located outside the system of charges. In the second case, the point at which the potential is zero is considered to be located inside the system of charges (between the charges).

Complete step by step answer:
From given, we have the data,
The amount of charge 1 = ${{q}_{1}}=5\mu C$
The amount of charge 2 = ${{q}_{2}}=-3\mu C$
The distance between the charges, d = 16 cm
d = 0.16 m
There are two cases:
Case I: A point at which the potential is zero is placed outside the system of charges.
Consider a point P outside the system of the charges at a distance x from the negative charge, where potential is zero.
Consider the arrangement of charges as follows:

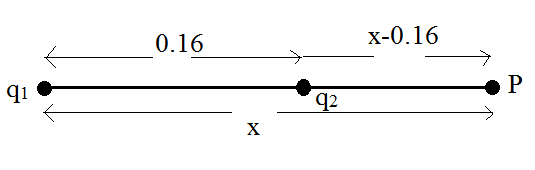
From the arrangement, the potential is given by,
$V=\dfrac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}x}+\dfrac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}(x-0.16)}$
For the potential being zero, the above equation reduces to,

& 0=\dfrac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}x}+\dfrac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}(x-0.16)} \\\ & \Rightarrow \dfrac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}x}=-\dfrac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}(x-0.16)} \\\ & \Rightarrow \dfrac{{{q}_{1}}}{x}=-\dfrac{{{q}_{2}}}{(x-0.16)} \\\ \end{aligned}$$ Substitute the values of the charges in the above equation to find the value of ‘x’. So, we get, $$\begin{aligned} & \dfrac{5\mu }{x}=-\dfrac{-3\mu }{(x-0.16)} \\\ & \Rightarrow \dfrac{5}{x}=\dfrac{3}{x-0.16} \\\ & \Rightarrow 5(x-0.16)=3x \\\ & \Rightarrow 5x-0.8=3x \\\ \end{aligned}$$ Rearrange the terms and find the value of ‘x’. $$\begin{aligned} & 5x-3x=0.8 \\\ & \Rightarrow 2x=0.8 \\\ & \Rightarrow x=0.4\,m \\\ \end{aligned}$$ Therefore, the value of x is 40 cm. Case II: A point at which the potential is zero is placed inside the system of charges. Consider a point P inside the system of the charges at a distance x from the positive charge, where potential is zero. Consider the arrangement of charges as follows:  From the arrangement, the potential is given by, $$V=\dfrac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}x}+\dfrac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}(0.16-x)}$$ For the potential being zero, the above equation reduces to, $$\begin{aligned} & 0=\dfrac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}x}+\dfrac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}(0.16-x)} \\\ & \Rightarrow \dfrac{{{q}_{1}}}{4\pi {{\varepsilon }_{0}}x}=-\dfrac{{{q}_{2}}}{4\pi {{\varepsilon }_{0}}(0.16-x)} \\\ & \Rightarrow \dfrac{{{q}_{1}}}{x}=-\dfrac{{{q}_{2}}}{(0.16-x)} \\\ \end{aligned}$$ Substitute the values of the charges in the above equation to find the value of ‘x’. So, we get, $$\begin{aligned} & \dfrac{5\mu }{x}=-\dfrac{-3\mu }{(0.16-x)} \\\ & \Rightarrow \dfrac{5}{x}=\dfrac{3}{0.16-x} \\\ & \Rightarrow 5(0.16-x)=3x \\\ & \Rightarrow 0.8-5x=3x \\\ \end{aligned}$$ Rearrange the terms and find the value of ‘x’. $$\begin{aligned} & 5x+3x=0.8 \\\ & \Rightarrow 8x=0.8 \\\ & \Rightarrow x=0.1\,m \\\ \end{aligned}$$ Therefore, the value of x is 10 cm. **In the case where the point at which the potential is zero is considered to be outside is 40 cm from the positive charge. In the case where the point at which the potential is zero is considered to be inside is 10 cm from the positive charge.** **Note:** The things to be on your finger-tips for further information on solving these types of problems are: The units of the given parameters should be taken into consideration while solving the problem. The uniformity in the case of units of the parameters should be maintained.