Question
Question: Two charges \( 5\mu C \) and \( - 3\mu C \) are located \( 16cm \) apart. At what points on the line...
Two charges 5μC and −3μC are located 16cm apart. At what points on the line joining the two charges is the electric potential zero?
Solution
First draw a rough diagram as per the given statement. Then assume a point on the line joining the two charges and let the point mark as x cm away from 5μC charge. Then write the total potential at that assumed point and equate it with zero as the electric potential at that point is zero. On further solving we can find the value of x which is our required answer.
Complete answer:
Electric potential:
It is defined as the amount of work energy needed to move a unit electric change from one point to another specific point in an electric field.
Formula of the electric potential:
V=4πε01×dq
Where,
V is the electric potential of the charge.
4πε01 is a constant term which we can replace with k.
The charge is equal to q.
The distance at which we are calculating the electric potential of the charge is d.
As per the given problem we have two charges 5μC and −3μC are located 16cm apart. Now we need to calculate the point on the line joining the two charges where the net electric potential due to these point charges is zero.
Let us assume a point which is x distance from the change 5μC on the line where the net electric potential is zero.
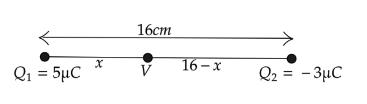
The electric potential at point x due to 5μC is,
V5=xkq5
Now putting the known value we will get,
V5=xk(5μC)……(1)
If the distance is x from cgnafe 5μC the for change −3μC the distance will be 16−x as the toa distance between the two p[pint is 16cm
The electric potential at point 16−x due to −3μC is,
V−3=16−xkq−3
Now putting the known value we will get,
V−3=16−xk(−3μC)……(2)
Now the net electric potential at that point be,
V=V5+V−3
Putting equation (1) and (2) we will get,
V=xk(5μC)+16−xk(−3μC)
⇒V=xk(5μC)−16−xk(3μC)
As per the problem the electric potential at that point is zero.
Now,
0=xk(5μC)−16−xk(3μC)
⇒xk(5μC)=16−xk(3μC)
Cancelling the common term we will get,
x5=16−x3
Rearranging the term we will get,
5(16−x)=3x
⇒80−5x=3x
⇒80=3x+5x⇒x=880=10cm
Hence the point from the −3μC will be (16−x)=16−10=6cm .
Note:
Here in the above problem we assume the given point x inside the line joins two charges. If we assume that point outside of the line joining two points. Where the net potential will be zero.
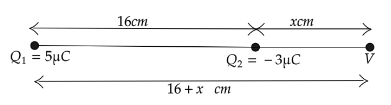
V5=(16+x)k(5μC)……(1)
V−3=xk(−3μC)……(2)
Net electric potential be,
V=V5+V−3
Putting values,
V=(16+x)k(5μC)+xk(−3μC)=(16+x)k(5μC)−xk(3μC)
Equatind net electric potential to zero,
0=(16+x)k(5μC)−xk(3μC)
⇒(16+x)k(5μC)=xk(3μC)
Canceling the common terms we will get,
(16+x)(5)=x(3)
Rearranging,
5x=3(16+x)
On solving we will get,
x=12cm which is the distance from −3μC change.
Hence the distance from the 5μC charge be 16+x=16+12=40cm .
