Question

Two charges 2μC and −2μC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?

Answer 1

Since there are two charges given and both the charges are opposite in nature, this means that the equipotential surface will have the zero potential as both charges are different, they will cancel out the influence of each other. If they are the same charges then the equipotential surface will be the point where the influence from both of them is the same.

Complete step by step solution:
We have been given that
${{q}_{1}}=2\mu C=2\times {{10}^{-6}}C$
${{q}_{2}}=-2\mu C=-2\times {{10}^{-6}}C$
Distance (r) = 0.06 m
A.) In the first part we need to find the equipotential surface, which means that the potential will be zero at that point due to both the charges
Let “x” be the point in between both the charges where potential is zero
Therefore, by using formula
$\dfrac{1}{4\pi {{\varepsilon }_{0}}}[\dfrac{{{q}_{1}}}{x}+\dfrac{{{q}_{2}}}{(0.06-x)}]=0$
$\dfrac{{{q}_{1}}}{x}=-\dfrac{{{q}_{2}}}{(0.06-x)}$
$\dfrac{2\times {{10}^{-6}}}{x}=\dfrac{-2\times {{10}^{-6}}}{(0.06-x)}$
On solving this, we get
x = 0.03 m
This means that the midpoint of the imaginary straight line passing through both the charges will be the equipotential surface for both the charges. The above illustration, can be diagrammatically shown as below

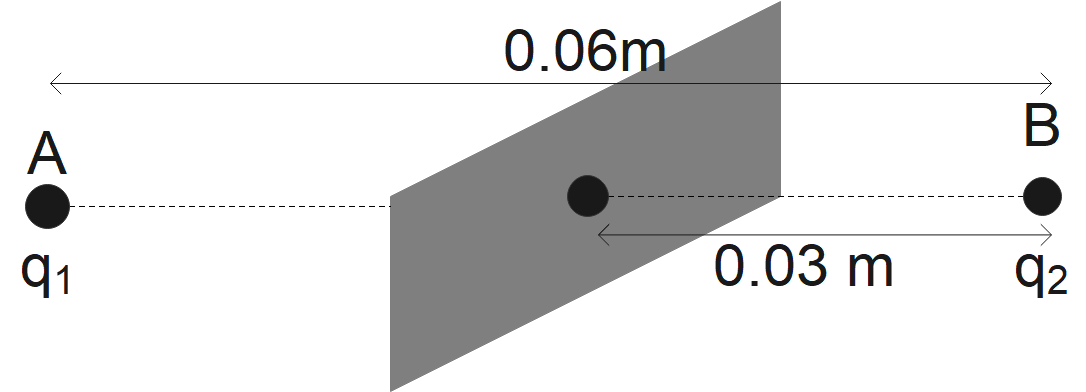
B.) In this part we have been asked about the direction at every point on the surface. Since we all know that the force and field act perpendicular to each other hence, we can say that the electric field will act normal to the plane in the direction of AB as shown in above figure

Note: Since, in the second part we have been asked about the direction of the field and hence, we can say that the potential will be in the direction of the field. Since in the above figure we have found the equipotential surface this means that the field will be in that direction only.