Question

Two charges $2.0 \times {10^{ - 6}}\,{\text{C}}$ and $1.0 \times {10^{ - 6}}\,{\text{C}}$ are placed at a separation of $10\,{\text{cm}}$. Where should a third charge be placed Such that it experiences no net force due to these charges?

Answer 1

Use the formula for the electrostatic force between the two charges. This formula gives the relation between the magnitudes of the two charges and distance between the two charges. The third charge experiences no net force hence the electrostatic force of attraction between the first charge and third charge as well the between the second charge and the third charge should be equal.
Formula used:
The electrostatic force $F$ of attraction between two charges is given by
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$ …… (1)
Here, $k$ is a constant, ${q_1}$ and ${q_2}$ are the magnitudes of two charges and $r$ is the distance between the two charges.

Complete step by step answer:
Let ${q_1}$ and ${q_2}$ be the two charges with magnitudes $2.0 \times {10^{ - 6}}\,{\text{C}}$ and $1.0 \times {10^{ - 6}}\,{\text{C}}$ placed at a distance $10\,{\text{cm}}$i.e. $0.1\,{\text{m}}$ from each other.

Since the net force between the charges becomes zero, the third charge should be placed somewhere in between the two charges.

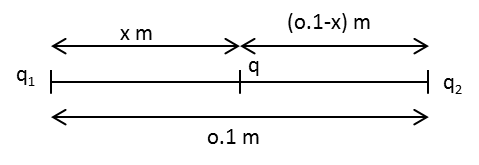
Let $q$ bet the third charge at distances $x\,{\text{m}}$ and $\left( {0.1 - x} \right)\,{\text{m}}$ from the charges ${q_1}$ and ${q_2}$ respectively.

The electrostatic force ${F_1}$ between the charges ${q_1}$ and $q$ is
${F_1} = \dfrac{{k{q_1}q}}{{{{\left( {x\,{\text{m}}} \right)}^2}}}$

The electrostatic force ${F_2}$ between the charges ${q_2}$ and $q$ is
${F_2} = \dfrac{{k{q_2}q}}{{{{\left[ {\left( {0.1 - x} \right)\,{\text{m}}} \right]}^2}}}$

Since the third charge $q$ experiences no force due to the charges ${q_1}$ and ${q_2}$. The forces ${F_1}$ and ${F_2}$ must be equal.
${F_1} = {F_2}$

Substitute $\dfrac{{k{q_1}q}}{{{{\left( {x\,{\text{m}}} \right)}^2}}}$ for ${F_1}$ and $\dfrac{{k{q_2}q}}{{{{\left[ {\left( {0.1 - x} \right)\,{\text{m}}} \right]}^2}}}$ for ${F_2}$ in the above equation.
$\dfrac{{k{q_1}q}}{{{{\left( {x\,{\text{m}}} \right)}^2}}} = \dfrac{{k{q_2}q}}{{{{\left[ {\left( {0.1 - x} \right)\,{\text{m}}} \right]}^2}}}$
$\Rightarrow \dfrac{{{q_1}}}{{{{\left( {x\,{\text{m}}} \right)}^2}}} = \dfrac{{{q_2}}}{{{{\left[ {\left( {0.1 - x} \right)\,{\text{m}}} \right]}^2}}}$

Substitute $2.0 \times {10^{ - 6}}\,{\text{C}}$ for ${q_1}$ and $1.0 \times {10^{ - 6}}\,{\text{C}}$ for ${q_2}$ in the above equation.
$\dfrac{{2.0 \times {{10}^{ - 6}}\,{\text{C}}}}{{{{\left( {x\,{\text{m}}} \right)}^2}}} = \dfrac{{1.0 \times {{10}^{ - 6}}\,{\text{C}}}}{{{{\left[ {\left( {0.1 - x} \right)\,{\text{m}}} \right]}^2}}}$
$\Rightarrow \dfrac{2}{{{x^2}}} = \dfrac{1}{{{{\left( {0.1 - x} \right)}^2}}}$
$\Rightarrow 2{\left( {0.1 - x} \right)^2} = {x^2}$
$\Rightarrow x = \sqrt 2 \left( {0.1 - x} \right)$
$\Rightarrow x = 0.1\sqrt 2 - \sqrt 2 x$
$\Rightarrow \sqrt 2 x + x = 0.1\sqrt 2$
$\Rightarrow x = \dfrac{{0.1\sqrt 2 }}{{1 + \sqrt 2 }}$
$\Rightarrow x = 0.0585\,{\text{m}}$
$\Rightarrow x \approx 0.059\,{\text{m}}$
Convert the unit of distance in centimeters.
$x = \left( {0.059\,{\text{m}}} \right)\left( {\dfrac{{{{10}^2}\,{\text{cm}}}}{{1\,{\text{m}}}}} \right)$
$\Rightarrow x = 5.9\,{\text{cm}}$
Hence, the distance of the third charge should be $5.9\,{\text{cm}}$ from the charge $2.0 \times {10^{ - 6}}\,{\text{C}}$.

Note:
The constant is the same for both the forces between the three charges. Hence, it gets cancelled when two forces are equated. Also convert the unit of distance between two charges in meters as all the units are in the SI system of units.