Question

Two charged particles $q$ and $4q$ are kept at distance $3\;m$ as shown in figure.

The force on charge $Q$ placed at point $P$ is:
A. $5kQq$
B. $kQq$
C. $2k{q^2}$
D. Zero

Answer 1

When a charged particle comes in the range of other point charges in that region then it experiences a force on it due to the point charges present in that region. The formula for the electrostatic force due to other charged particles is applied along with the concept of Coulomb’s law in order to determine the total force on charge $Q$. The net force on the charged particle considered will be the total force exerted on it by both the point charges.

Formula used:
The Coulomb’s force is given by the equation:
$\vec F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
Where, $k$ is the electrostatic force constant, ${q_1}$ is the test charge or the charge which is considered, ${q_2}$ is the other point charge in the range of the test charge and $r$ is the distance of separation between the charged particles.

Complete step by step answer:
The above problem revolves around the concept of Coulomb’s law. In order to find out the force on the charged particle $Q$ we first need to know the concept behind Coulomb’s law and when it is applied. Now we will apply the principle of Coulomb’s law. Coulomb's law states that the force of attraction or repulsion between two stationary point charges is directly proportional to the product of magnitudes of the two charges and inversely proportional to the square of the distance between them.

The electrostatic force applied on the test charge by a point charge separated by a distance is given by a formula given by Coulomb’s law and hence this equation is:
$\vec F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$ -------($1$)
Let us now extract the data given in the question. The distances between the respective point charges and the charge $Q$ are given. The value of electrostatic constant $k$ is said to be a constant.

Given, $k = 9 \times {10^9}$, ${r_1} = 1\;m$ and ${r_2} =2\;m$. When there is a presence of a charged particle in the region of one or more point charges an electric field is definitely produced in accordance with Coulomb's law. When a charged particle is placed on an axis in the presence of two other charged particles then it is said to experience some force called as the electrostatic force which is due to the two other charged particles in its region, that is, $q$ and $4q$ as seen in the diagram.

When a charged particle is brought in the range of other point charges having some charge then this charged particle is said to get affected. The particle considered here, that is, charged particle $Q$ is said to be called a test charge. A test charge is said to be a positively charged particle on which the number of forces exerted due to other point charges are considered. The question says that this charged particle $Q$ is placed at point $P$ which is shown in the diagram below.

force due to the point charges $q$ and $4q$ which are also said to be positive in nature. This is because as per the basic properties of electrostatics, charges are said to repel each other. Hence there are two forces that are exerted on the test charge $Q$. One is due to the point charge $q$ and the one is due to the point charge $4q$.

Since the force is a vector quantity it is said to have magnitude and some direction. Hence the direction is also considered here. Since the force is said to be repulsive in nature then we can say that the force due to point charge $q$ on $Q$ will be away from it and the same applies for the force due to point charge $4q$ on $Q$. This is illustrated in the diagram shown below:

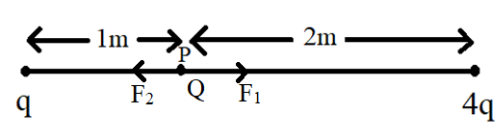
The ${\vec F_1}$ force on $Q$ is due to the point charge $q$ and the force ${\vec F_2}$ is due to the point charge $4q$. The net force on $Q$ will be the sum of the forces exerted on the test charge. Since the forces are in opposite directions the net force will be the difference between them. However, the magnitudes of these forces will be different and hence the force with a greater magnitude is considered to have a greater value. Hence, the net force is determined by subtracting the force with a comparatively smaller magnitude from the force with the greater magnitude.

From the equation ($1$) we can see that the Coulomb force and the distance of separation between the charged particles are inversely related to each other. So greater the distance lesser is the magnitude of force. Since the distance between $q$ and $Q$ is lesser than the distance between $Q$ and $4q$ (as seen from diagram), the force ${\vec F_1}$ on $Q$ is due to the point charge $q$ is greater in magnitude than ${\vec F_2}$.
Hence,
${\vec F_{net}} = {\vec F_1} - {\vec F_2}$ --------($2$)
We now apply the equation ($1$) to determine the value of force ${\vec F_1}$. Since force on $Q$ is due to $q$ we get:
${\vec F_1} = \dfrac{{kQq}}{{{r^2}}}$ --------($3$)
Now, we apply the equation ($1$) to determine the value of force ${\vec F_2}$. Since this force on $Q$ is due to $4q$ we get:
${\vec F_2} = \dfrac{{kQ(4q)}}{{{r^2}}}$
$\Rightarrow {\vec F_2} = \dfrac{{4kQq}}{{{r^2}}}$ ---------($4$)
We now substitute equations ($3$) and ($4$) in equation ($1$) to get:
${\vec F_{net}} = \dfrac{{kQq}}{{{r^2}}} - \dfrac{{4kQq}}{{{r^2}}}$

By taking out the $Q$ and $q$ we get:
${\vec F_{net}} = qQ\left[ {\dfrac{k}{{{r^2}}} - \dfrac{{4k}}{{{r^2}}}} \right]$
By substituting the given values we get:
${\vec F_{net}} = qQ\left[ {\dfrac{{9 \times {{10}^9}}}{{{{\left( 1 \right)}^2}}} - \dfrac{{4 \times 9 \times {{10}^9}}}{{{{\left( 2 \right)}^2}}}} \right]$
By solving further we get:
${\vec F_{net}} = qQ\left[ {\dfrac{{9 \times {{10}^9}}}{1} - \dfrac{{4 \times 9 \times {{10}^9}}}{4}} \right]$
$\Rightarrow {\vec F_{net}} = qQ\left[ {9 \times {{10}^9} - 9 \times {{10}^9}} \right]$
$\Rightarrow {\vec F_{net}} = qQ\left( 0 \right)$
$\therefore {\vec F_{net}} = 0$
Hence, the total force exerted on charge $Q$ placed at point $P$ by point charges $q$ and $4q$ is $0$.

Therefore, the correct option is option D.

Note: A common error which is observed in the above problem is that the direction of the electrostatic force exerted on $Q$ is not considered which is wrong. The net force is calculated just by subtracting the two forces from each other which is not correct because the force with a comparatively smaller magnitude is subtracted from the force with a greater magnitude and not vice-versa. To do this the directions of the force must be considered. The direction of the net force will always be in the direction of the force with a greater magnitude.