Question
Question: Two charged particles are projected as in figure. The minimum value of \(d\) for which they do not c...
Two charged particles are projected as in figure. The minimum value of d for which they do not collide-
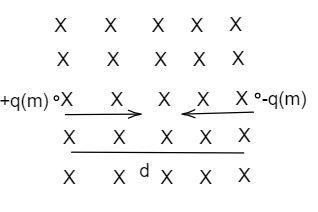
(1) d>qBm(v1+v2)
(2) d<qBm(v1+v2)
(3) d>qB2m(v1+v2)
(4) d<qB2m(v1+v2)
Solution
Write the formula of the radius of the rotation of the charged particle given below. Substitute the value of the velocity of both the particles in the formula. The radius of the rotation of the given two charged particles in a circular path is the same.
Formula used: The formula of the radius of the circular path of the charge is given by
r=qBmv
Where r is the radius of the circular path of the charges, m is the mass of the charges, v is the velocity of the charges , q is the charge and B is the magnetic field.
Complete step by step solution
It is known that the distance d may include the half of the circular path of two charges. Hence the value of the d is twice that of the radius. Hence it is written as
d=2r
d=2(qBmv)
The total velocity of the charged particles is the sum of the velocity of the individual particles. Let us consider that the velocity of the first charged particle is v1 and the velocity of the second charged particle is v2 . Hence their total velocity is v1+v2 . Substituting this total velocity in the above equation, we get
d=2qBm(v1+v2)
The obtained d value is the maximum, for the minimum case, the radius of the circular path is enough to remain collide. Hence
d=r
d>qBm(v1+v2)
Thus the option (1) is correct.
Note: The greater than symbol is preferred since the value of the distance must be greater than the radius of the circular path of either one of the charged particles. Otherwise the charged particles may collide each other. In this both the charged particle is located on the same side of rotation.
